文章编号:11272时间:2024-09-30人气:

Material Components 是一个由 Google 开发的组件库,用于构建遵循 Material Design 原则的 Android 应用。该组件库提供了一系列可复用的组件,例如按钮、文本字段、卡片和底部导航栏,可以帮助你快速轻松地构建美观且一致的应用。
Material Components 允许你高度定制其组件,以匹配你的应用的品牌和风格。你可以通过以下方式进行定制:
Material Components 经过优化,可以提高 Android 应用的性能。它使用轻量级代码库和高效的渲染技术,以最大程度地减少应用程序的大小和内存使用量。该组件库还提供了一系列性能优化技巧,例如:
Material Components 符合 Web Content Accessibility Guidelines (WCAG) 标准,以确保你的
要开始使用 Material Components,请按照以下步骤操作:
有关更多详细信息,请参阅Material Components for Android 官方文档。
以下是一个使用 Material Components 创建文本字段的示例:
Material Components 是一个功能强大且易于使用的组件库,可以帮助你构建美观、高效且可访问的 Android 应用。通过提供定制化、性能优化和可访问性功能,Material Components 使你能够快速轻松地创建出色的用户体验。
在 Google 的 I/O 大会上,Material Design 系统迎来了重要更新Material Design 3,特别是在个性化功能上展现了全新的表现力。 Material You 的发布展示了动态颜色支持和组件升级,包括颜色扩展和主题更新。 以下是迁移和应用 Material Design 3 的关键点:
1. 主题迁移: 从M2到M3(MDC 1.4.0到1.5.0),更新主题为Material 3,将.*替换为3.*,同时更新部件样式。
2. 颜色与主题: Material You扩展了颜色空间,引入第三色和从主色等衍生的插值色。 动态颜色可通过Material Theme Builder简化配置,并支持Web和Figma的可视化。
3. 动态色彩生成: Material You在Android 12中根据壁纸自动生成动态调色板,根据用户选择分析颜色并应用到主题属性中,确保对比度和可访问性。
4. 代码整合: 应用中需确保无硬编码颜色,动态颜色通过DynamicColors类管理,如在()中添加一行动态颜色应用代码。
5. 排版调整: Material 3简化了标题、字幕等样式,分为小、中、大三个等级,文本样式更规则。
6. 组件更新: 如Top App Bar使用新表面色调,Bottom Navigation View的图标和标签颜色变化,FAB设计更新为圆角矩形等。
现在是时候将你的UI库升级到Material Design 3,探索更加丰富和个性化的用户体验了。
一、基本技术 ----------------------------------------------------- 1)MATLAB索引或引用(MATLAB Indexing or Referencing) 在MATLAB中有三种基本方法可以选取一个矩阵的子阵。 它们分别是 下标法,线性法和逻辑法(subscripted, linear, and logical)。 如果你已经熟悉这个内容,请跳过本节 1.1)下标法 非常简单,看几个例子就好。 A = 6:12; A([3,5]) ans = 8 10 A([3:2:end]) ans = 8 10 12 A = [11 14 17; ... 12 15 18; ... 13 16 19]; A(2:3,2) ans = 15 16 1.2)线性法 二维矩阵以列优先顺序可以线性展开,可以通过现行展开后的元素序号 来访问元素。 A = [11 14 17; ... 12 15 18; ... 13 16 19]; A(6) ans = 16 A([3,1,8]) ans = 13 11 18 A([3;1;8]) ans = 13 11 18 1.3)逻辑法 用一个和原矩阵具有相同尺寸的0-1矩阵,可以索引元素。 在某个 位置上为1表示选取元素,否则不选。 得到的结果是一个向量。 A = 6:10; A(logical([0 0 1 0 1])) ans = 8 10 A = [1 2 3 4]; B = [1 0 0 1]; A(logical(B)) ans = 1 4 ----------------------------------------------------- 2)数组操作和矩阵操作(Array Operations vs. Matrix Operations) 对矩阵的元素一个一个孤立进行的操作称作数组操作;而把矩阵视为 一个整体进行的运算则成为矩阵操作。 MATLAB运算符*,/,,^都是矩阵 运算,而相应的数组操作则是.*, ./, ., .^ A=[1 0 ;0 1]; B=[0 1 ;1 0]; A*B % 矩阵乘法 ans = 0 1 1 0 A.*B % A和B对应项相乘 ans = 0 0 0 0 ------------------------------------------------------ 3)布朗数组操作(Boolean Array Operations) 对矩阵的比较运算是数组操作,也就是说,是对每个元素孤立进行的。 因此其结果就不是一个“真”或者“假”,而是一堆“真假”。 这个 结果就是布朗数组。 D = [-0.2 1.0 1.5 3.0 -1.0 4.2 3.14]; D >= 0 ans = 0 1 1 1 0 1 1 如果想选出D中的正元素: D = D(D>0) D = 1.0000 1.5000 3.0000 4.2000 3.1400 除此之外,MATLAB运算中会出现NaN,Inf,-Inf。 对它们的比较参见下例 Inf==Inf返回真 Inf<1返回假 NaN==NaN返回假 同时,可以用isinf,isnan判断,用法可以顾名思义。 在比较两个矩阵大小时,矩阵必须具有相同的尺寸,否则会报错。 这是 你用的上size和isequal,isequalwithequalnans(R13及以后)。 ------------------------------------------------------ 4)从向量构建矩阵(Constructing Matrices from Vectors) 在MATLAB中创建常数矩阵非常简单,大家经常使用的是: A = ones(5,5)*10 但你是否知道,这个乘法是不必要的? A = 10; A = A(ones(5,5)) A = 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 类似的例子还有: v = (1:5); n = 3; M = v(:,ones(n,1)) M = 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 事实上,上述过程还有一种更加容易理解的实现方法: A = repmat(10,[5 5]); M = repmat([1:5], [1,3]); 其中repmat的含义是把一个矩阵重复平铺,生成较大矩阵。 更多详细情况,参见函数repmat和meshgrid。 ----------------------------------------------------- 5)相关函数列表(Utility Functions) ones 全1矩阵 zeros 全0矩阵 reshape 修改矩阵形状 repmat 矩阵平铺 meshgrid 3维plot需要用到的X-Y网格矩阵 ndgrid n维plot需要用到的X-Y-Z...网格矩阵 filter 一维数字滤波器,当数组元素前后相关时特别有用。 cumsum 数组元素的逐步累计 cumprod 数组元素的逐步累计 eye 单位矩阵 diag 生成对角矩阵或者求矩阵对角线 spdiags 稀疏对角矩阵 gallery 不同类型矩阵库 Pascal Pascal 矩阵 hankel Hankel 矩阵 toeplitz Toeplitz 矩阵 ========================================================== 二、扩充的例子 ------------------------------------------------------ 6)作用于两个向量的矩阵函数 假设我们要计算两个变量的函数F F(x,y) = x*exp(-x^2 - y^2) 我们有一系列x值,保存在x向量中,同时我们还有一系列y值。 我们要对向量x上的每个点和向量y上的每个点计算F值。 换句话 说,我们要计算对于给定向量x和y的所确定的网格上的F值。 使用meshgrid,我们可以复制x和y来建立合适的输入向量。 然后 可以使用第2节中的方法来计算这个函数。 x = (-2:.2:2); y = (-1.5:.2:1.5); [X,Y] = meshgrid(x, y); F = X .* exp(-X.^2 - Y.^2); 如果函数F具有某些性质,你甚至可以不用meshgrid,比如 F(x,y) = x*y ,则可以直接用向量外积 x = (-2:2); y = (-1.5:.5:1.5); x*y 在用两个向量建立矩阵时,在有些情况下,稀疏矩阵可以更加有 效地利用存储空间,并实现有效的算法。 我们将在第8节中以一个 实例来进行更详细地讨论. -------------------------------------------------------- 7)排序、设置和计数(Ordering, Setting, and Counting Operations) 在迄今为止讨论过的例子中,对向量中一个元素的计算都是独立 于同一向量的其他元素的。 但是,在许多应用中,你要做的计算 则可能与其它元素密切相关。 例如,假设你用一个向量x来表示一 个集合。 不观察向量的其他元素,你并不知道某个元素是不是一 个冗余元素,并应该被去掉。 如何在不使用循环语句的情况下删除 冗余元素,至少在现在,并不是一个明显可以解决的问题。 解决这类问题需要相当的智巧。 以下介绍一些可用的基本工具 max 最大元素 min 最小元素 sort 递增排序 unique 寻找集合中互异元素(去掉相同元素) diff 差分运算符[X(2) - X(1), X(3) - X(2), ... X(n) - X(n-1)] find 查找非零、非NaN元素的索引值 union 集合并 intersect 集合交 setdiff 集合差 setxor 集合异或 继续我们的实例,消除向量中的多余元素。 注意:一旦向量排序后, 任何多余的元素就是相邻的了。 同时,在任何相等的相邻元素在向量 diff运算时变为零。 这是我们能够应用以下策略达到目的。 我们现在 在已排序向量中,选取那些差分非零的元素。 % 初次尝试。 不太正确! x = sort(x(:)); difference = diff(x); y = x(difference~=0); 这离正确结果很近了,但是我们忘了diff函数返回向量的元素个数比 输入向量少1。 在我们的初次尝试中,没有考虑到最后一个元素也可能 是相异的。 为了解决这个问题,我们可以在进行差分之前给向量x加入 一个元素,并且使得它与以前的元素一定不同。 一种实现的方法是增 加一个NaN。 % 最终的版本。 x = sort(x(:)); difference = diff([x;NaN]); y = x(difference~=0); 我们使用(:)运算来保证x是一个向量。 我们使用~=0运算,而不用find 函数,因为find函数不返回NaN元素的索引值,而我们操作中差分的最 后元素一定是NaN。 这一实例还有另一种实现方式: y=unique(x); 后者当然很简单,但是前者作为一个练习并非无用,它是为了练习使用 矢量化技术,并示范如何编写你自己的高效代码。 此外,前者还有一个 作用:Unique函数提供了一些超出我们要求的额外功能,这可能降低代 码的执行速度。 假设我们不只是要返回集合x,而且要知道在原始的矩阵里每个相异元素 出现了多少个“复本”。 一旦我们对x排序并进行了差分,我们可以用 find来确定差分变化的位置。 再将这个变化位置进行差分,就可以得到 复本的数目。 这就是diff of find of diff的技巧。 基于以上的讨论, 我们有: % Find the redundancy in a vector x x = sort(x(:)); difference = diff([x;max(x)+1]); count = diff(find([1;difference])); y = x(find(difference)); plot(y,count) 这个图画出了x中每个相异元素出现的复本数。 注意,在这里我们避开了 NaN,因为find不返回NaN元素的索引值。 但是,作为特例,NaN和Inf 的复本数可以容易地计算出来: count_nans = sum(isnan(x(:))); count_infs = sum(isinf(x(:))); 另一个用于求和或者计数运算的矢量化技巧是用类似建立稀疏矩阵的方 法实现的。 这还将在第9节中作更加详细的讨论. ------------------------------------------------------- 8)稀疏矩阵结构(Sparse Matrix Structures) 在某些情况下,你可以使用稀疏矩阵来增加计算的效率。 如果你构造一 个大的中间矩阵,通常矢量化更加容易。 在某些情况下,你可以充分利 用稀疏矩阵结构来矢量化代码,而对于这个中间矩阵不需要大的存储空 间。 假设在上一个例子中,你事先知道集合y的域是整数的子集, {k+1,k+2,...k+n};即, y = (1:n) + k 例如,这样的数据可能代表一个调色板的索引值。 然后,你就可以对集 合中每个元素的出现进行计数(构建色彩直方图?译者)。 这是对上一 节中diff of find of diff技巧的一种变形。 现在让我们来构造一个大的m x n矩阵A,这里m是原始x向量中的元素数, n是集合y中的元素数。 A(i,j) = 1 if x(i) = y(j) 0 otherwise 回想一下第3节和第4节,你可能认为我们需要从x和y来构造矩阵A。 如果 当然可以,但要消耗许多存储空间。 我们可以做得更好,因为我们知道, 矩阵A中的多数元素为0,x中的每个元素对应的行上只有一个值为1。 以下就是构造矩阵的方法(注意到y(j) = k+j,根据以上的公式): x = sort(x(:)); A = sparse(1:length(x), x+k, 1, length(x), n); 现在我们对A的列进行求和,得到出现次数。 count = sum(A); 在这种情况下,我们不必明确地形成排序向量y,因为我们事先知道 y = 1:n + k. 这里的关键是使用数据,(也就是说,用x控制矩阵A的结构)。 由于x在 一个已知范围内取整数值,我们可以更加有效地构造矩阵。 假设你要给一个很大矩阵的每一列乘以相同的向量。 使用稀疏矩阵,不仅 可以节省空间,并且要比在第5节介绍的方法更加快速. 下面是它的工作 方式: F = rand(1024,1024); x = rand(1024,1); % 对F的所有行进行点型乘法. Y = F * diag(sparse(x)); % 对F的所有列进行点型乘法. Y = diag(sparse(x)) * F; 我们充分利用矩阵乘法算符来执行大规模运算,并使用稀疏矩阵以防止临 时变量变得太大。 -------------------------------------------------------- 9)附加的例子(Additional Examples) 下面的例子使用一些在本技术手册中讨论过的方法,以及其它一些相关方 法。 请尝试使用tic 和toc(或t=cputime和cputime-t),看一下速度加快 的效果。 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 用于计算数组的双重for循环。 使用的工具:数组乘法 优化前: A = magic(100); B = pascal(100); for j = 1:100 for k = 1:100; X(j,k) = sqrt(A(j,k)) * (B(j,k) - 1); end end 优化后: A = magic(100); B = pascal(100); X = sqrt(A).*(B-1); >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 用一个循环建立一个向量,其元素依赖于前一个元素 使用的工具:FILTER, CUMSUM, CUMPROD 优化前: A = 1; L = 1000; for i = 1:L A(i+1) = 2*A(i)+1; end 优化后: L = 1000; A = filter([1],[1 -2],ones(1,L+1)); >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 如果你的向量构造只使用加法或乘法,你可使用cumsum或cumprod函数。 优化前: n=; V_B=100*ones(1,n); V_B2=100*ones(1,n); ScaleFactor=rand(1,n-1); for i = 2:n V_B(i) = V_B(i-1)*(1+ScaleFactor(i-1)); end for i=2:n V_B2(i) = V_B2(i-1)+3; end 优化后: n=; V_A=100*ones(1,n); V_A2 = 100*ones(1,n); ScaleFactor=rand(1,n-1); V_A=cumprod([100 1+ScaleFactor]); V_A2=cumsum([100 3*ones(1,n-1)]); >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 向量累加,每5个元素进行一次: 工具:CUMSUM , 向量索引 优化前: % Use an arbitrary vector, x x = 1; y = []; for n = 5:5:length(x) y = [y sum(x(1:n))]; end 优化后(使用预分配): x = 1; ylength = (length(x) - mod(length(x),5))/5; % Avoid using ZEROS command during preallocation y(1:ylength) = 0; for n = 5:5:length(x) y(n/5) = sum(x(1:n)); end 优化后(使用矢量化,不再需要预分配): x = 1; cums = cumsum(x); y = cums(5:5:length(x)); >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 操作一个向量,当某个元素的后继元素为0时,重复这个元素: 工具:FIND, CUMSUM, DIFF 任务:我们要操作一个由非零数值和零组成的向量,要求把零替换成为 它前面的非零数值。 例如,我们要转换下面的向量: a=2; b=3; c=5; d=15; e=11; x = [a 0 0 0 b 0 0 c 0 0 0 0 d 0 e 0 0 0 0 0]; 为: x = [a a a a b b b c c c c c d d e e e e e e]; 解(diff和cumsum是反函数): valind = find(x); x(valind(2:end)) = diff(x(valind)); x = cumsum(x); >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 将向量的元素累加到特定位置上 工具:SPARSE 优化前: % The values we are summing at designated indices values = [20 15 45 50 75 10 15 15 35 40 10]; % The indices associated with the values are summed cumulatively indices = [2 4 4 1 3 4 2 1 3 3 1]; totals = zeros(max(indices),1); for n = 1:length(indices) totals(indices(n)) = totals(indices(n)) + values(n); end 优化后: indices = [2 4 4 1 3 4 2 1 3 3 1]; totals = full(sparse(indices,1,values)); 注意:这一方法开辟了稀疏矩阵的新用途。 在使用sparse命令创建稀疏矩阵 时,它是对分配到同一个索引的所有值求和,而不是替代已有的数值。 这称 为向量累加,是MATLAB处理稀疏矩阵的方式。

MATLAB具备卓越的数值计算能力外,它还提供了专业水平的符号计算,文字处理,可视化建模仿真和实时控制等功能。 你可以看看这个: MATLAB的基本数据单位是矩阵,它的指令表达式与数学,工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完相同的事情简捷得多.在新的版本中也加入了对C,FORTRAN,c++ ,JAVA的支持.可以直接调用,用户也可以将自己编写的实用程序导入到MATLAB函数库中方便自己以后调用,此外许多的MATLAB爱好者都编写了一些经典的程序,用户可以直接进行下载就可以用,非常的方便。 MATLAB的基础是矩阵计算,但是由于他的开放性,并且mathwork也吸收了像maple等软件的优点,使MATLAB成为一个强大的数学软件当前流行的MATLAB 6.5/7.0包括拥有数百个内部函数的主包和三十几种工具包(Toolbox).工具包又可以分为功能性工具包和学科工具包.功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能.学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类.开放性使MATLAB广受用户欢迎.除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包的官方网站:的优势和特点(1)友好的工作平台和编程环境MATLAB由一系列工具组成。 这些工具方便用户使用MATLAB的函数和文件,其中许多工具采用的是图形用户界面。 包括MATLAB桌面和命令窗口、历史命令窗口、编辑器和调试器、路径搜索和用于用户浏览帮助、工作空间、文件的浏览器。 随着MATLAB的商业化以及软件本身的不断升级,MATLAB的用户界面也越来越精致,更加接近Windows的标准界面,人机交互性更强,操作更简单。 而且新版本的MATLAB提供了完整的联机查询、帮助系统,极大的方便了用户的使用。 简单的编程环境提供了比较完备的调试系统,程序不必经过编译就可以直接运行,而且能够及时地报告出现的错误及进行出错原因分析。 (2)简单易用的程序语言Matlab一个高级的距阵/阵列语言,它包含控制语句、函数、数据结构、输入和输出和面向对象编程特点。 用户可以在命令窗口中将输入语句与执行命令同步,也可以先编写好一个较大的复杂的应用程序(M文件)后再一起运行。 新版本的MATLAB语言是基于最为流行的C++语言基础上的,因此语法特征与C++语言极为相似,而且更加简单,更加符合科技人员对数学表达式的书写格式。 使之更利于非计算机专业的科技人员使用。 而且这种语言可移植性好、可拓展性极强,这也是MATLAB能够深入到科学研究及工程计算各个领域的重要原因。 (3)强大的科学计算机数据处理能力MATLAB是一个包含大量计算算法的集合。 其拥有600多个工程中要用到的数学运算函数,可以方便的实现用户所需的各种计算功能。 函数中所使用的算法都是科研和工程计算中的最新研究成果,而前经过了各种优化和容错处理。 在通常情况下,可以用它来代替底层编程语言,如C和C++ 。 在计算要求相同的情况下,使用MATLAB的编程工作量会大大减少。 MATLAB的这些函数集包括从最简单最基本的函数到诸如距阵,特征向量、快速傅立叶变换的复杂函数。 函数所能解决的问题其大致包括矩阵运算和线性方程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和其他初等数学运算、多维数组操作以及建模动态仿真等。 (4)出色的图形处理功能MATLAB自产生之日起就具有方便的数据可视化功能,以将向量和距阵用图形表现出来,并且可以对图形进行标注和打印。 高层次的作图包括二维和三维的可视化、图象处理、动画和表达式作图。 可用于科学计算和工程绘图。 新版本的MATLAB对整个图形处理功能作了很大的改进和完善,使他不仅在一般数据可视化软件都具有的功能(例如二维曲线和三维曲面的绘制和处理等)方面更加完善,而且对于一些其他软件所没有的功能(例如图形的光照处理、色度处理以及四维数据的表现等),MATLAB同样表现了出色的处理能力。 同时对一些特殊的可视化要求,例如图形对话等,MATLAB也有相应的功能函数,保证了用户不同层次的要求。 另外新版本的MATLAB还着重在图形用户界面(GUI)的制作上作了很大的改善,对这方面有特殊要求的用户也可以得到满足。 (5)应用广泛的模块集合工具箱MATLAB对许多专门的领域都开发了功能强大的模块集和工具箱。 一般来说,他们都是由特定领域的专家开发的,用户可以直接使用工具箱学习、应用和评估不同的方法而不需要自己编写代码。 目前,MATLAB已经把工具箱延伸到了科学研究和工程应用的诸多领域,诸如数据采集、数据库接口、概率统计、样条拟合、优化算法、偏微分方程求解、神经网络、小波分析、信号处理、图像处理、系统辨识、控制系统设计、LMI控制、鲁棒控制、模型预测、模糊逻辑、金融分析、地图工具、非线性控制设计、实时快速原型及半物理仿真、嵌入式系统开发、定点仿真、DSP与通讯、电力系统仿真等,都在工具箱(Toolbox)家族中有了自己的一席之地。 (6)实用的程序接口和发布平台新版本的MATLAB可以利用MATLAB编译器和C/C++数学库和图形库,将自己的MATLAB程序自动转换为独立于MATLAB运行的C和C++代码。 允许用户编写可以和MATLAB进行交互的C或C++语言程序。 另外,MATLAB网页服务程序还容许在Web应用中使用自己的MATLAB数学和图形程序。 MATLAB的一个重要特色就是他有一套程序扩展系统和一组称之为工具箱的特殊应用子程序。 工具箱是MATLAB函数的子程序库,每一个工具箱都是为某一类学科专业和应用而定制的,主要包括信号处理、控制系统、神经网络、模糊逻辑、小波分析和系统仿真等方面的应用。 (7)应用软件开发(包括用户界面)在开发环境中,使用户更方便地控制多个文件和图形窗口;在编程方面支持了函数嵌套,有条件中断等;在图形化方面,有了更强大的图形标注和处理功能,包括对性对起连接注释等;在输入输出方面,可以直接向Excel和HDF5。 (8) Matlab常用工具箱介绍(英汉对照)Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱System Identification Toolbox——系统辨识工具箱Wavele Toolbox——小波工具箱例如:控制系统工具箱包含如下功能:连续系统设计和离散系统设计状态空间和传递函数以及模型转换时域响应(脉冲响应、阶跃响应、斜坡响应)频域响应(Bode图、Nyquist图)根轨迹、极点配置1.补充新的内容:MATLAB R2007b正式发布了!MATLAB 2007b于2007年秋节正式发布,TMW正式发布了MATLAB R2007b,新版本涵盖:Simulink 7、新产品Simulink Design Verifier、Link for Analog Devices VisualDSP以及82个产品模块的更新升级及Bug修订。 从现在开始,MathWorks公司将每年进行两次产品发布,时间分别在每年的3月和9 月,而且,每一次发布都会包含所有的产品模块,如产品的new feature、bug fixes和新产品模块的推出。 在R2007b中(MATLAB 7.4,Simulink 6.6),主要更新了多个产品模块、增加了多达350个新特性、增加了对64位Windows的支持,并新推出了工具箱。 R2007b, released on March 1, 2007, includes updates to MATLAB and Simulink, two new products released since R2007b, and updates and bug fixes to 82 other products. R2007b adds support for the Intel® based Mac, Windows Vista™, and 64-bit Sun Solaris™ SPARC platforms.这次的升级做了重大的增强,也升级了以下各版本,提供了MATLAB、SIMULINK的升级以及其他最新的模块的升级。 这个Matlab 2007版本不仅仅提高了产品质量,同时也提供了新的用于数据分析、大规模建模、固定点开发、编码等新特征。 其中MATLAB Builder for 扩展了MATLAB Compiler的功能,主要有: 可以打包MATLAB函数,使网络程序员可以通过C#,等语言访问这些函数; 创建组件来保持MATLAB的灵活性; 创建COM组件; 将源自MATLAB函数的错误作为一个标准的管理异常来处理。 R2007b 提供了重大的新功能: 直接在命令行使用 Real-Time Workshop 的 嵌入式 MATLAB 函数的 C 代码生成。 另外,Simulink 中的嵌入式 MATLAB 函数块支持多 M 文件中的算法。 MATLAB R2007b新版本中,产品模块进行了一些调整,MATLAB Builder for COM的功能集成到MATLAB Builder for 中去了,Finacial Time Series Toolbox的功能集成到Financial Toolbox中了。 MATLAB 将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作,而且利用 MATLAB 产品的开放式结构,可以非常容易地对 MATLAB 的功能进行扩充,从而在不断深化对问题认识的同时,不断完善 MATLAB 产品以提高产品自身的竞争能力。 作为和Mathematica、Maple并列的三大数学软件。 其强项就是其强大的矩阵计算以及仿真能力。 要知道Matlab的由来就是Matrix + Laboratory = Matlab,所以这个软件在国内也被称作《矩阵实验室》。 每次MathWorks发布Matlab的同时也会发布仿真工具Simulink。 在欧美很多大公司在将产品投入实际使用之前都会进行仿真试验,他们所主要使用的仿真软件就是Simulink。 Matlab提供了自己的编译器:全面兼容C++以及 Fortran两大语言。 所以Matlab是工程师,科研工作者手上最好的语言,最好的工具和环境。 Matlab 已经成为广大科研人员的最值得信赖的助手和朋友!
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/24b0f8028bbfcc6a63b0.html,复制请保留版权链接!
随着AppleWatch的发布,移动应用程序开发又进入了一个令人兴奋的新时代,WatchOS应用程序是专为AppleWatch设计的,提供了令人兴奋的新方式来与用户互动,如果您是一名iOS开发人员,那么学习如何构建和部署WatchOS应用程序将是一个明智的举动,因为它可以大大扩展您的技能并为您打开新的机会,先决条件Xcode6iOS设...。
互联网资讯 2024-09-28 23:01:21

最小生成树的概念最小生成树,MST,是一个加权、连通、无向图的生成树,其中生成树的边权和最小,生成树是一个包含原图中所有顶点的子图,并且满足以下条件,无回路连通所有边权和最小克鲁斯卡尔算法克鲁斯卡尔算法是一种贪心算法,用于求解最小生成树问题,该算法的步骤如下,1.将图的边按权重从小到大排序,2.依次选择权重最小的边添加到生成树中,直到...。
最新资讯 2024-09-27 00:40:22

在当今数字时代,文件大小的不断增加对我们的存储空间和网络带宽提出了越来越大的挑战,为了应对这一挑战,压缩技术应运而生,旨在减少文件大小,同时尽可能保持数据完整性,Zzip是一项领先的压缩技术,一直致力于提供更高的压缩率,从而进一步缩减文件大小,压缩率的作用压缩率是指压缩后的文件大小与原始文件大小之比,压缩率越高,压缩后的文件就越小,需...。
技术教程 2024-09-26 10:44:41

帕斯卡是一种强大的编程语言,非常适合游戏开发,它拥有丰富的库,专门用于创建交互式和引人入胜的游戏体验,本指南将带你了解帕斯卡游戏开发的基础知识,从安装和设置开发环境到创建和部署你的游戏,安装和设置要开始使用帕斯卡进行游戏开发,你需要安装帕斯卡编译器和一个集成开发环境,IDE,流行的IDE包括Lazarus和Delphi,安装完成后,...。
技术教程 2024-09-26 07:30:53

简介在Android开发中,应用程序的生命周期是一个至关重要的概念,它定义了应用程序从启动到关闭所经历的不同状态以及这些状态之间的转换,了解应用程序的生命周期对于构建健壮且高效的应用程序至关重要,应用程序状态应用程序有四种主要状态,Created,应用程序已创建,但尚未可见,Started,应用程序可见并处于活动状态,Paused,应...。
本站公告 2024-09-17 02:42:07

在快速发展的技术领域,持续学习对于保持编程技术的更新至关重要,编程语言、框架和技术不断更新换代,因此养成持续学习的习惯对于软件开发人员来说至关重要,持续学习的好处保持技能相关性,持续学习有助于确保您的技能与当前行业需求保持相关性,从而提高您的就业能力和竞争力,解决新问题,学习新的技术和方法可以为您提供解决新问题和克服编程挑战所需的新视...。
最新资讯 2024-09-15 20:41:48

是一种低级汇编语言,可以在Web浏览器中运行,为JavaScript提供更快的性能,探索JavaScript的新姿势除了以上介绍的基本和高级概念外,JavaScript还不断演进,涌现出新的姿势和应用场景,其中一个值得关注的领域是Java反序列化绕WAF技术,Java反序列化是一种将Java对象转换为字节流并重新创建的过程,这种技术通...。
技术教程 2024-09-14 00:03:30
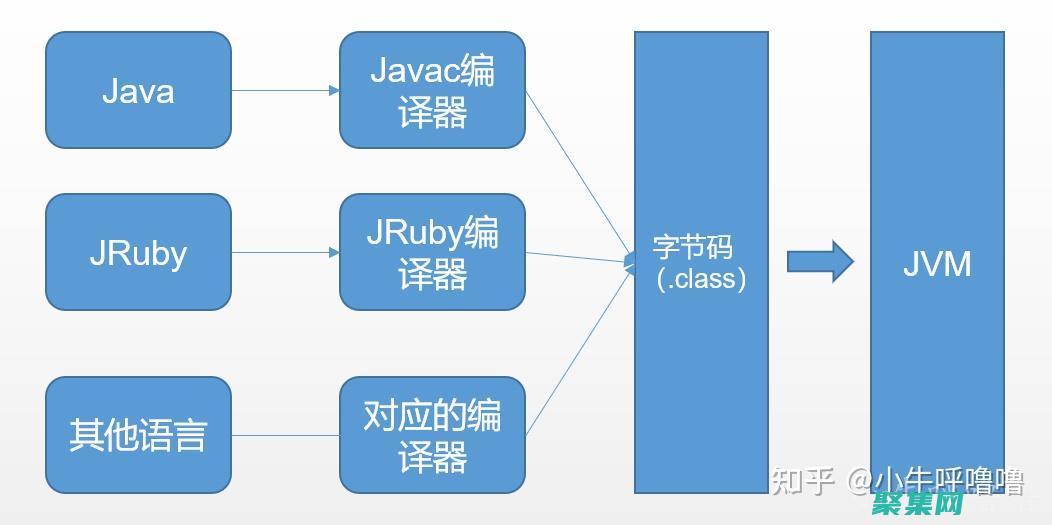
在Java虚拟机,JVM,中,垃圾回收,GC,是至关重要的机制,负责管理内存并回收不再使用的对象,JVM使用各种算法来执行GC,从而确保应用程序的平稳运行和内存的有效利用,让我们深入分析一下这些算法的工作原理,串行垃圾回收串行垃圾回收是最简单的GC算法,它对整个堆进行单线程扫描,JVM暂停所有应用程序线程,扫描堆以识别不再使用的对象,...。
互联网资讯 2024-09-12 22:55:41

人工智能,AI,软件正在飞速发展,许多企业和个人都在寻找使用AI软件的方法来提高效率和生产力,对于刚开始使用AI软件的人来说,弄清楚如何开始使用它们可能会令人生畏,本指南将介绍使用AI软件的基础知识,并提供一些提示,帮助你充分利用AI的潜力,选择合适的AI软件第一步是选择满足你需求的AI软件,有各种各样的AI软件可用,从专注于特定任务...。
技术教程 2024-09-12 07:08:16
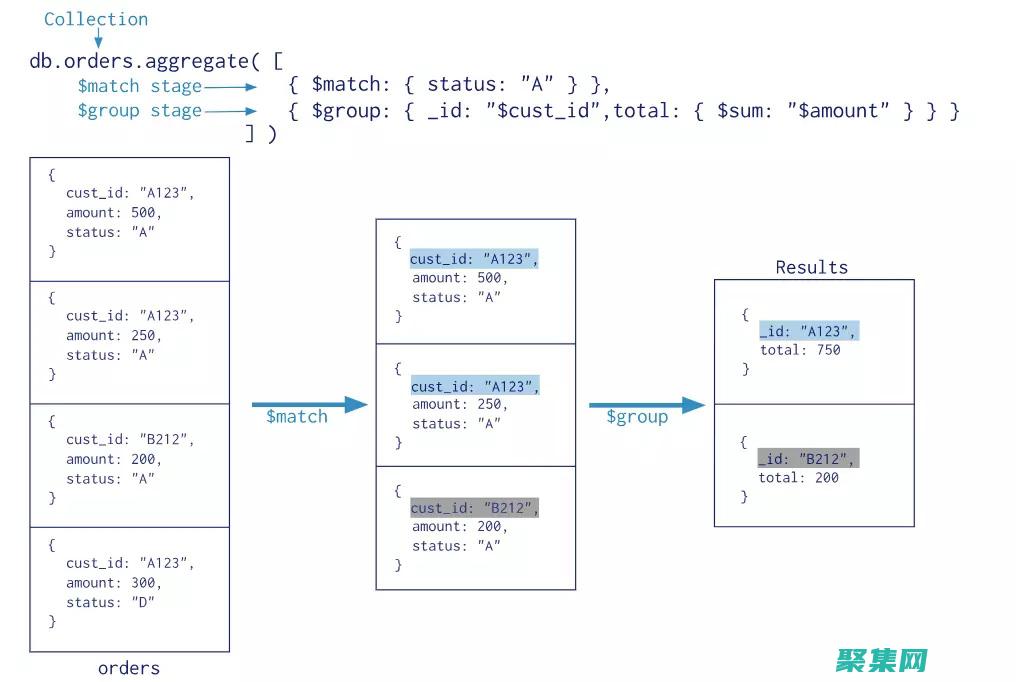
引言聚合函数是数据分析中用于对大数据集执行计算的重要工具,它们可以执行求和、计数、最大值和最小值等操作,并返回一个单个值作为结果,在分布式系统中,聚合函数需要扩展才能处理大规模数据集,聚合函数分组使用方法在分布式系统中扩展聚合函数的一种常见方法是使用分组技术,分组将数据集分成较小的块,并在每个块上单独计算聚合函数,将每个块的聚合结果组...。
互联网资讯 2024-09-10 11:02:48

引言在Java中,常量是指值在编译时确定的变量,它们对于确保应用程序的健壮性非常重要,特别是在多线程环境中,本文将探讨Java中的常量,并解释为什么不可变性对于并行编程至关重要,什么是常量,常量是值不能被修改的变量,在Java中,常量可以通过使用`final`关键字来声明,例如,javapublicfinalintNUM,THREAD...。
技术教程 2024-09-07 21:28:30

在广州繁华热闹的闹市中,荔湾广场矗立着一座宏伟的建筑,凭借着优越的地理位置和丰富的购物选择,它成为了许多当地人和游客的购物天堂,在荔湾广场光鲜亮丽的外表之下,隐藏着一段鲜为人知的过去,为这座繁华的商场披上了一层阴森的色彩,昔日的刑场在荔湾广场建成之前,这片区域曾是清末广州的刑场,无数的罪犯在此被处决,他们的怨气在土地上留下难以磨灭的印...。
互联网资讯 2024-09-05 03:54:45