文章编号:4483时间:2024-09-11人气:
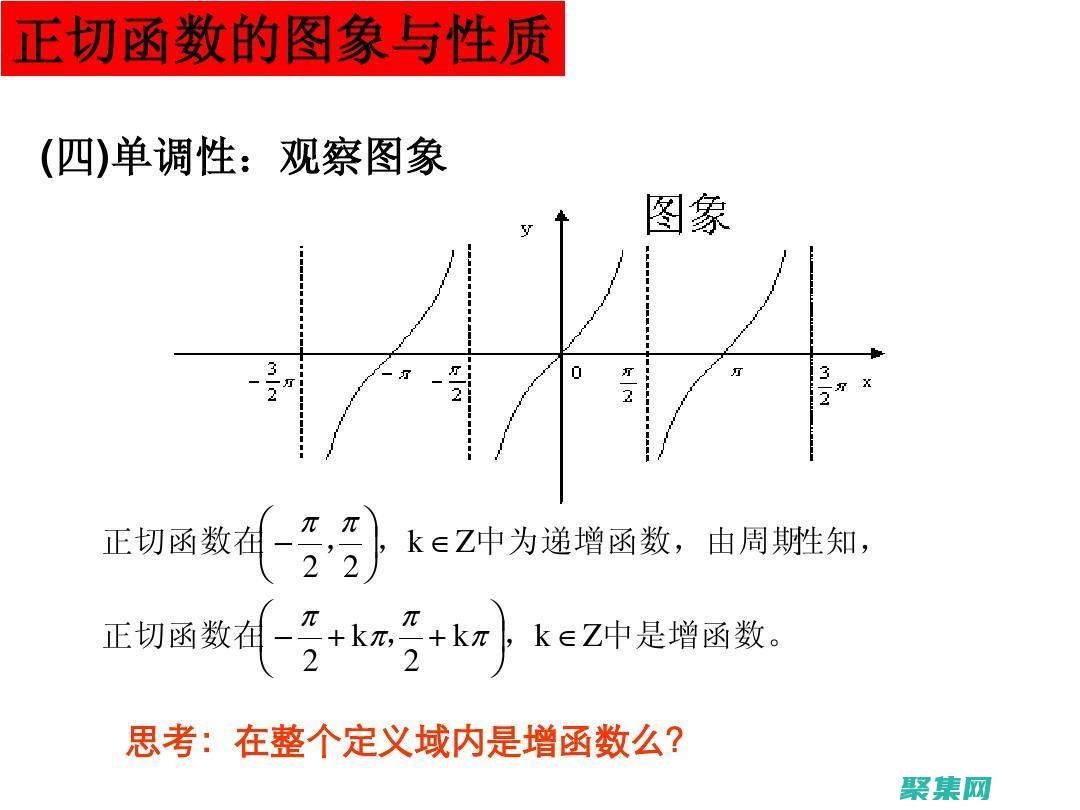
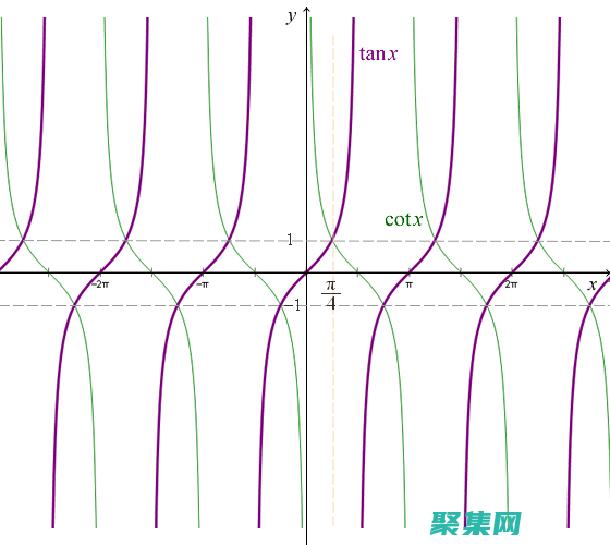
余切函数 (tan) 是三角学中一个重要的函数,它表示一个角的正切值。在本篇文章中,我们将介绍余切函数的三角学表示和解析表示,并提供相应的证明。
 证明:
使用正余弦表示,我们可以将余切函数写成:```tan(θ ± φ) = (sin(θ ± φ)) / (cos(θ ± φ))```使用角的和差公式展开正弦和余弦函数,得到:```tan(θ ± φ) = (sin θ cos φ ± cos θ sin φ) / (cos θ cos φ∓ sin θ sin φ)```整理分母,得到:```tan(θ ± φ) = (sin θ cos φ ± cos θ sin φ) / (cos θ cos φ - sin θ sin φ)```使用分配律和余切函数的定义,得到:```tan(θ ± φ) = (tan θ cos φ ± tan φ) / (1 ± tan θ tan φ)```因此,得证。
证明:
使用正余弦表示,我们可以将余切函数写成:```tan(θ ± φ) = (sin(θ ± φ)) / (cos(θ ± φ))```使用角的和差公式展开正弦和余弦函数,得到:```tan(θ ± φ) = (sin θ cos φ ± cos θ sin φ) / (cos θ cos φ∓ sin θ sin φ)```整理分母,得到:```tan(θ ± φ) = (sin θ cos φ ± cos θ sin φ) / (cos θ cos φ - sin θ sin φ)```使用分配律和余切函数的定义,得到:```tan(θ ± φ) = (tan θ cos φ ± tan φ) / (1 ± tan θ tan φ)```因此,得证。
 证明:
使用欧拉公式,我们可以写出:```e^(ix) = cos(x) + i sin(x)```将 e^(ix) 代入余切函数的三角学表示中,得到:```tan(x) = (cos(x) + i sin(x)) / (cos(x) - i sin(x))```将分母分母同时乘以共轭复数 cos(x) + i sin(x),得到:```tan(x) = ((cos(x) + i sin(x))^2) / (cos(x)^2 + sin(x)^2)```使用三角恒等式简化分母,得到:```tan(x) = ((cos(x) + i sin(x))^2) / 1```展开平方,得到:```tan(x) = (cos(x)^2 + 2icos(x)sin(x) - sin(x)^2) / 1```使用三角恒等式简化分子,得到:```tan(x) = (e^(2ix) - 1) / (e^(2ix) + 1)```因此,得证。
证明:
使用欧拉公式,我们可以写出:```e^(ix) = cos(x) + i sin(x)```将 e^(ix) 代入余切函数的三角学表示中,得到:```tan(x) = (cos(x) + i sin(x)) / (cos(x) - i sin(x))```将分母分母同时乘以共轭复数 cos(x) + i sin(x),得到:```tan(x) = ((cos(x) + i sin(x))^2) / (cos(x)^2 + sin(x)^2)```使用三角恒等式简化分母,得到:```tan(x) = ((cos(x) + i sin(x))^2) / 1```展开平方,得到:```tan(x) = (cos(x)^2 + 2icos(x)sin(x) - sin(x)^2) / 1```使用三角恒等式简化分子,得到:```tan(x) = (e^(2ix) - 1) / (e^(2ix) + 1)```因此,得证。
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/9dc4612098c8a5f92851.html,复制请保留版权链接!

在Java中,您可以使用各种时钟工具来获取精确的时间,这些工具提供了不同级别的精度,并允许您处理时间相关任务,1.System.currentTimeMillis,此方法返回自纪元时间,1970年1月1日UTC,以来经过的毫秒数,它是最基本的时钟工具,精度为毫秒,longmillis=System.currentTimeMillis...。
技术教程 2024-09-11 05:34:18

只授予用户所需的最低权限是数据安全的重要原则,它意味着只授予用户执行其工作职责所需的访问权限,这有助于防止数据泄露和滥用,为什么只授予最低权限很重要,只授予最低权限很重要,因为,可以减少数据泄露的风险,如果用户只有所需的最低权限,那么他们泄露敏感数据的风险就较低,可以防止数据滥用,如果用户没有不必要的访问权限,那么他们就无法滥用数据,...。
本站公告 2024-09-10 10:46:07

简介NORM函数是MATLAB中一个多功能的数据处理工具,可用于计算数组或标量的绝对值,它比直接使用ABS函数更通用,因为NORM函数还可以指定符号,用法NORM函数的语法如下,norm,X,norm,X,P,norm,X,P,DIM,其中,X是要计算范数的数组或标量,P指定范数类型,P的有效值包括,1,计算1范数,即数组中元素的绝对...。
本站公告 2024-09-09 19:20:43

作为一名经验丰富的Java开发人员,与你合作可以为我带来许多好处,你的专业知识和经验可以帮助我快速提升技能,并让我对Java生态系统有更深入的理解,你的专业知识可以帮助我快速提升技能你对Java语言和库的深入理解可以帮助我提高代码质量和效率,你可以指导我使用最佳实践,遵循行业标准,并避免常见错误,你还可以向我介绍最新的Java技术和趋...。
技术教程 2024-09-08 22:15:11
PHP是一个广受欢迎的Web开发语言,以其强大的功能和易于使用的语法而闻名,PHP5.2.6是一个功能丰富的版本,提供了许多特性和增强功能,使其成为Web开发的理想选择,PHP5.2.6的优势提高效率,PHP5.2.6引入了许多性能改进,使应用程序运行更快、更高效,简化流程,它提供了一系列新函数和类,简化了常见任务并提高了开发效率,增...。
本站公告 2024-09-07 14:30:00

引言Java是一种面向对象的编程语言,以其跨平台、高效和易用的特点而闻名,它广泛应用于从企业应用程序到移动应用程序的各种领域,作为一名Java开发人员,掌握核心概念、最佳实践和高级技巧至关重要,教程将为您提供全面指南,帮助您提升您的Java技能,核心概念面向对象编程,OOP,Java是一种面向对象的语言,这意味着它围绕对象的概念组织...。
最新资讯 2024-09-07 13:01:25
对于初学者和经验丰富的程序员来说,编程网站都是一个宝贵的资源,可以帮助他们学习、成长和交流,从互动式课程到在线论坛,这些网站提供了各种各样的工具和资源,使你能够提高编程技能,在本文中,我们将为你介绍一些最顶尖的编程网站,这些网站将带你进入编程世界的无限可能,在线课程Coursera,Coursera提供来自世界顶尖大学和公司的广泛计算...。
技术教程 2024-09-07 09:48:27

JavaMissionControl,JMC,是Oracle提供的免费、开源的Java应用程序性能监控和故障排除工具,它是一个功能强大的工具,可以帮助您监视和管理Java应用程序的性能以及解决问题,JMC的特点实时监控应用程序的性能指标,如CPU使用率、内存使用率和线程活动,对代码进行采样,以识别应用程序中的性能瓶颈,使用火焰图可视化...。
最新资讯 2024-09-07 09:42:57

使用javac编译时的处理步骤当使用javac编译时,调用代码需要经过以下几个处理步骤,词法分析,此步骤将源代码分解为称为标记的离散单元,例如关键字、标识符和运算符,语法分析,此步骤将标记组装成称为语法树的层级结构,语法树表示源代码的语法结构,语义分析,此步骤检查语法树的语义,以确保代码在语法上正确且语义上有效,字节码生成,此步骤将语...。
本站公告 2024-09-06 19:00:31
JavaScript是一种强大的编程语言,可用于在网页上创建各种特效,从简单的过渡动画到复杂的三维交互,JavaScript可以帮助您提升网站的视觉效果,增强用户体验,探索JavaScript特效淡入淡出放大缩小旋转移动悬停拖放淡入淡出放大缩小旋转移动悬停拖放,定义特效函数functionfadeIn,element,elemen...。
互联网资讯 2024-09-05 23:42:14

在广袤无垠的中国土地上,流传着数千年的灵异传说和神秘事件,这些事件,有的已被科学证实,有的仍是未解之谜,激发了人们对未知领域的无尽探索,以下列出了15个最令人难以置信的中国灵异事件,带您领略这个神秘莫测的世界,1.昆仑山死亡谷位于青藏高原腹地的昆仑山,以其令人毛骨悚然的死亡谷而闻名,据传,这个神秘的山谷里隐藏着许多磁场异常,导致人类和...。
互联网资讯 2024-09-04 01:39:47
成都网站建设有成都建站有限公司、成都网络公司、嘻嘻网络科技、创企科技、龙兵科技等,1、成都建站有限公司成都网站设计科技有限公司主要从事网站设计、网站建设、网站制作、网站开发、企业建站等业务,是一个专业的网站建设公司,提供手机网站建设,让网站在移动端也有很好的展现,公司还提供完整的网站建设合同和网站建设规划书,真正做到为客户服务,2、成...。
技术教程 2024-09-02 02:26:07