多项式拟合在机器学习和人工智能中的应用：从理论到实践 (多项式拟合在线)

简介

多项式拟合是一种机器学习技术，用于拟合数据点到多项式曲线。它是一种强大的工具，可以用于各种应用，包括回归分析、曲线拟合和预测。在本文中，我们将探讨多项式拟合在机器学习和人工智能中的应用。我们将从理论基础开始，然后讨论实际应用以及使用多项式拟合的代码示例。

理论基础

多项式拟合的目标是找到一个多项式函数，它最能拟合一组数据点。对于给定的数据点 {(x1, y1), (x2, y2), ..., (xn, yn)}, 多项式函数的方程为：```f(x) = a0 + a1 x + a2 x^2 + ... + an x^n```其中，a0, a1, ..., an 是多项式的系数。为了找到最佳拟合的多项式，我们需要最小化多项式函数与数据点的误差。通常使用均方误差 (MSE) 作为误差度量：```MSE = (1/n) Σ(yi - f(xi))^2```其中，n 是数据点的数量。为了最小化 MSE，我们可以使用优化算法，例如梯度下降或牛顿法。通过迭代更新多项式的系数，我们可以找到最能拟合数据点的多项式。

实际应用

多项式拟合在机器学习和人工智能中具有广泛的应用。以下是其中一些最常见的应用：

1. 回归分析： 多项式拟合可用于拟合数据点到线性或非线性趋势线。这对于预测未来值或确定变量之间的关系非常有用。

2. 曲线拟合： 多项式拟合可用于拟合复杂曲线。这对于医学成像、语音识别和计算机图形等应用非常有用。
3. 预测： 一旦拟合了多项式函数，就可以用来预测新数据点。这对于时间序列分析和财务预测等应用非常有用。

代码示例

以下是用 Python 实现多项式拟合的代码示例：```pythonimport numpy as npfrom sklearn.linear_model import LinearRegression生成数据点x = np.linspace(0, 10, 100)y = 3 x2 + 2 x + 1 + np.random.normal(0, 0.1, 100)拟合多项式函数model = LinearRegression()model.fit(x.reshape(-1, 1), y)评估拟合结果print("拟合多项式：", model.coef_)print("拟合均方误差：", np.mean((y - model.predict(x.reshape(-1, 1)))2))预测新数据点new_x = 5new_y = model.predict([[new_x]])print("预测值为：", new_y)```

结论

多项式拟合是一种强大的机器学习技术，可以用于各种应用。通过了解其理论基础和实际应用，我们可以利用多项式拟合来解决复杂问题并做出准确的预测。

---

人工智能、计算智能、机器学习的关系？

揭开人工智能、计算智能与机器学习的神秘面纱

人工智能（AI）这一概念，如同一座宏大的知识宫殿，涵盖了模拟人类智能的理论与技术，从机器人到语言识别，它的分支繁多，包括弱AI、强AI和潜在的超级智能。 AI的根基在于强大的算力、精准的算法以及海量的数据，而其中最为璀璨的明珠便是机器学习，它犹如AI海洋中的一朵浪花，专研于计算机自我学习的奥秘。

机器学习的多元世界

机器学习的领域广泛，它包括监督学习（如回归和分类，通过有标签数据指导模型学习）、无监督学习（如聚类和概率图模型，探索未知数据的内在结构），以及强化学习，让计算机在与环境互动中自我优化。 监督学习的代表算法有支持向量机和线性回归，而决策树和随机森林则是监督学习中的佼佼者。 无监督学习如PCA和K-means聚类，以及层次聚类，共同助力模式识别，尤其是K-means，基于距离的算法，DBSCAN则凭借密度连接挖掘出隐藏的结构。

数据驱动的探索之旅

机器学习的实践旅程始于数据的获取，重要的是避免过拟合并确保数据质量。 数据处理环节包括清洗和标准化，为模型选择和训练奠定坚实基础。 模型训练过程中，梯度下降法如影随形，模型评估则通过交叉验证来检验其稳健性。 参数调优是关键步骤，超参数搜索让模型适应性更强。 最后，模型在测试集上进行预测，验证其在未知数据上的表现。

人工智能的深度技术

AI的核心技术之一，深度学习，以多层感知器和深层神经网络为核心，能处理复杂数据并学习内在规律。 卷积神经网络等应用更是展现了深度学习的威力，尤其在图像处理和自然语言处理（NLP）中大放异彩。 而联邦学习，是一种创新的加密分布式学习方式，保护数据隐私的同时，共享模型的智慧。 计算机视觉和机器视觉，分别聚焦于模仿人类视觉和结合图像分析与机械工程的智能应用。

总的来说，人工智能、计算智能与机器学习相互交织，共同构建了现代科技的基石。 深入探索它们的边界，我们不仅能在科技的海洋中游刃有余，更能推动人类社会向更智能、更高效的方向前进。 如果你对这些领域感兴趣，[行行查]提供了详尽的资料，让我们一起在知识的田野上探索前行。

全基因组选择之模型篇

在介绍GS模型之前，我们有必要先来了解一下混合线性模型（Mixed Linear Model，MLM）。 混合线性模型是一种方差分量模型，既然是线性模型，意味着各量之间的关系是线性的，可以应用叠加原理，即几个不同的输入量同时作用于系统的响应，等于几个输入量单独作用的响应之和（公式1）。

?= + =? +? ? +? ? +⋯+? ? +?（公式1）

式中?表示响应变量的测量值向量， 为固定效应自变量的设计矩阵， 是与 对应的固定效应参数向量；? 、? 、⋯、? 是未知参数；? 、? 、⋯、? 是影响各因素的观察值；?是残差。同时需要满足条件： E(y)=Xβ，Var(y)=σ I， y 服从正态分布。

既然是混合效应模型，则既含有固定效应，又含有随机效应。 所谓固定效应是指所有可能出现的等级或水平是已知且能观察的，如性别、年龄、品种等。 所谓随机效应是指随机从总体中抽取样本时可能出现的水平，是不确定的，如个体加性效应、母体效应等（公式2）。

= + +? （公式2）

式中 为观测值向量； 为固定效应向量； 为随机效应向量，服从均值向量为0、方差协方差矩阵为G的正态分布 ； 为固定效应的关联矩阵； 为随机效应的关联矩阵；?为随机误差向量，其元素不必为独立同分布，即 。同时假定 Cov(G,R)=0 ，即G与R间无相关关系， 的方差协方差矩阵变为 Var(y)=ZGZ+R 。若 不存在，则为固定效应模型。若 不存在，则为随机效应模型。

在传统的线性模型中，除线性关系外，响应变量还有正态性、独立性和方差齐性的假定。 混合线性模型既保留了传统线性模型中的正态性假定条件，又对独立性和方差齐性不作要求，从而扩大了适用范围，目前已广泛应用于基因组选择。

很早以前就在理论上提出了最佳线性无偏预测（Best Linear Unbiased Prediction，BLUP）的统计方法，但由于计算技术滞后限制了应用。 直到上世纪70年代中期，计算机技术的发展为BLUP在育种中的应用提供了可能。 BLUP结合了最小二乘法的优点，在协方差矩阵已知的情况下，BLUP是分析动植物育种目标性状理想的方法，其名称含义如下：

在混合线性模型中，BLUP是对随机效应中随机因子的预测，BLUE（Best Linear Unbiased Estimation）则是对固定效应中的固定因子的估算。 在同一个方程组中既能对固定效应进行估计，又能对随机遗传效应进行预测。

BLUP方法最初应用在动物育种上。 传统的动物模型是基于系谱信息构建的亲缘关系矩阵（又称A矩阵）来求解混合模型方程组（Mixed Model Equations，MME）的，因此称之ABLUP。 Henderson提出的MME如下所示：

式中X为固定效应矩阵，Z为随机效应矩阵，Y为观测值矩阵。其中R和G：

其中A为亲缘关系矩阵，因此可转化公式为：

进一步可转化为：

通过求解方程组，计算残差和加性方差的方差组分，即可得到固定因子效应值(BLUE)和随机因子效应值(BLUP)。

作为传统BLUP方法，ABLUP完全基于系谱信息来构建亲缘关系矩阵，进而求得育种值，此方法在早期动物育种中应用较多，现在已基本不单独使用。

VanRaden于2008年提出了基于G矩阵的GBLUP（Genomic Best Linear unbiased prediction）方法，G矩阵由所有SNP标记构建，公式如下：

GBLUP通过构建基因组关系矩阵G代替基于系谱信息构建的亲缘关系矩阵A，进而直接估算个体育种值。

GBLUP求解过程同传统BLUP方法，仅仅在G矩阵构建不同。 除了VanRaden的基因组关系构建G矩阵外，还有其他G矩阵构建方法，但应用最多的还是VanRaden提出的方法。 如Yang等提出的按权重计算G矩阵：

Goddard等提出的基于系谱A矩阵计算G矩阵：

目前GBLUP已经广泛应用于动植物育种中，并且因为它的高效、稳健等优点，现在仍饱受青睐。 GBLUP假设所有标记对G矩阵具有相同的效应，而在实际基因组范围中只有少量标记具有主效应，大部分标记效应较小，因此GBLUP仍有很大的改进空间。

在动物育种中，由于各种各样的原因导致大量具有系谱记录和表型信息的个体没有基因型，单步法GBLUP（single-step GBLUP，ssGBLUP）就是解决育种群体中无基因型个体和有基因型个体的基因组育种值估计问题。

ssGBLUP将传统BLUP和GBLUP结合起来，即把基于系谱信息的亲缘关系矩阵A和基因组关系矩阵G进行整合，建立新的关系矩阵H，达到同时估计有基因型和无基因型个体的育种值。

H矩阵构建方法：

式中w为加权因子，即多基因遗传效应所占比例。

构建H矩阵后，其求解MME过程也是与传统BLUP一样：

ssBLUP由于基因分型个体同时含有系谱记录和表型数据，相对于GBLUP往往具有更高的准确性。 该方法已成为当前动物育种中最常用的动物模型之一。 在植物育种中，往往缺乏较全面的系谱信息，群体中个体的基因型也容易被测定，因此没有推广开来。

如果把GBLUP中构建协变量的个体亲缘关系矩阵换成SNP标记构成的关系矩阵，构建模型，然后对个体进行预测，这就是RRBLUP（Ridge Regression Best Linear Unbiased Prediction）的思路。

为什么不直接用最小二乘法？最小二乘法将标记效应假定为 固定效应 ，分段对所有SNP进行回归，然后将每段中显著的SNP效应相加得到个体基因组育种值。 该方法只考虑了少数显著SNP的效应，很容易导致多重共线性和过拟合。

RRBLUP是一种改良的最小二乘法，它能估计出所有SNP的效应值。 该方法将标记效应假定为 随机效应 且服从正态分布，利用线性混合模型估算每个标记的效应值，然后将每个标记效应相加即得到个体估计育种值。

一般而言，基因型数据中标记数目远大于样本数（p>>n）。 RRBLUP因为是以标记为单位进行计算的，其运行时间相比GBLUP更长，准确性相当。

GBLUP是直接法的代表，它把个体作为随机效应，参考群体和预测群体遗传信息构建的亲缘关系矩阵作为方差协方差矩阵，通过迭代法估计方差组分，进而求解混合模型获取待预测个体的估计育种值。 RRBLUP是间接法的代表，它首先计算每个标记效应值，再对效应值进行累加，进而求得育种值。 下图比较了两类方法的异同：

直接法估计，间接法估计标记效应之和 M 。 当K=M’M且标记效应g服从独立正态分布（如上图所示）时，两种方法估计的育种值是一样的，即= M 。

基于BLUP理论的基因组选择方法假定所有标记都具有相同的遗传方差，而实际上在全基因组范围内只有少数SNP有效应，且与影响性状的QTL连锁，大多数SNP是无效应的。 当我们将标记效应的方差假定为某种先验分布时，模型变成了贝叶斯方法。 常见的贝叶斯方法也是Meuwissen提出来的（就是提出GS的那个人），主要有BayesA、BayesB、BayesC、Bayesian Lasso等。

BayesA假设每个SNP都有效应且服从正态分布，效应方差服从尺度逆卡方分布。 BayesA方法事先假定了两个与遗传相关的参数，自由度v和尺度参数S。 它将Gibbs抽样引入到马尔科夫链蒙特卡洛理论（MCMC）中来计算标记效应。

BayesB假设少数SNP有效应，且效应方差服从服从逆卡方分布，大多数SNP无效应（符合全基因组实际情况）。 BayesB方法的标记效应方差的先验分布使用混合分布，难以构建标记效应和方差各自的完全条件后验分布，因此BayesB使用Gibbs和MH（Metropolis-Hastings）抽样对标记效应和方差进行联合抽样。

BayesB方法在运算过程中引入一个参数π。 假定标记效应方差为0的概率为π，服从逆卡方分布的概率为1-π，当π为1时，所有SNP都有效应，即和BayesA等价。 当遗传变异受少数具有较大影响的QTL控制时，BayesB方法准确性较高。

BayesB中的参数π是人为设定的，会对结果带来主观影响。 BayesC、BayesCπ、BayesDπ等方法对BayesB进行了优化。 BayesC方法将π作为未知参数，假定其服从U(0,1)的均匀分布，并假设有效应的SNP的效应方差不同。 BayesCπ方法在BayesC的基础上假设SNP效应方差相同，并用Gibbs抽样进行求解。 BayesDπ方法对未知参数π和尺度参数S进行计算，假设S的先验分布和后验分布均服从(1,1)分布，可直接从后验分布中进行抽样。

下图较为形象地说明了不同方法的标记效应方差分布：

Bayesian Lasso（Least absolute shrinkage and selection operator）假设标记效应方差服从指数分布的正态分布，即拉普拉斯（Laplace）分布。 其与BayesA的区别在于标记效应服从的分布不同，BayesA假设标记效应服从正态分布。 Laplace分布可允许极大值或极小值以更大概率出现。

从以上各类贝叶斯方法可看出，贝叶斯方法的重点和难点在于如何对超参的先验分布进行合理的假设。

Bayes模型相比于BLUP方法往往具有更多的待估参数，在提高预测准确度的同时带来了更大的计算量。 MCMC需要数万次的迭代，每一次迭代需要重估所有标记效应值，该过程连续且不可并行，需消耗大量的计算时间，限制了其在时效性需求较强的动植物育种实践中的应用。

为提高运算速度和准确度，很多学者对Bayes方法中的先验假设和参数进行优化，提出了fastBayesA、BayesSSVS、fBayesB、emBayesR、EBL、BayesRS、BayesTA等。 但目前最常用的Bayes类方法还是上述的几种。

各种模型的预测准确度较大程度的取决于其模型假设是否适合所预测表型的遗传构建。 一般而言，调参后贝叶斯方法的准确性比BLUP类方法要略高，但运算速度和鲁棒性不如BLUP。 因此，我们应根据自身需求权衡利弊进行合理选择。

除了基于BLUP和Bayes理论的参数求解方法外，基因组选择还有半参数（如RKHS，见下篇）和非参数，如机器学习（Machine Learning, ML）等方法。 机器学习是人工智能的一个分支，其重点是通过将高度灵活的算法应用于观察到的个体（ 标记的数据 ）的已知属性（ 特征 ）和结果来预测未观察到的个体（ 未标记的数据 ）的结果。 结果可以是连续的，分类的或二元的。 在动植物育种中， 标记的数据 对应于具有基因型和表型的训练群体，而 未标记的数据 对应于测试群体，用于预测的 特征 是SNP基因型。

相比于传统统计方法，机器学习方法具有诸多优点：

支持向量机（Support Vector Machine，SVM）是典型的非参数方法，属于监督学习方法。 它既可解决分类问题，又可用于回归分析。 SVM基于结构风险最小化原则，兼顾了模型拟合和训练样本的复杂性，尤其是当我们对自己的群体数据不够了解时，SVM或许是基因组预测的备选方法。

SVM的基本思想是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。 在支持向量回归（Support Vector Regression，SVR）中，通常使用近似误差来代替像SVM中那样的最佳分离超平面和支持向量之间的余量。 假设ε为不敏感区域的线性损失函数，当测量值和预测值小于ε时，误差等于零。 SVR的目标就是同时最小化经验风险和权重的平方范数。 也就是说，通过最小化经验风险来估计超平面。

下图1比较了SVM中回归（图A）和分类（图B）的差别。 式中ξ和ξ*为松弛变量，C为用户定义的常数，W为权重向量范数，ϕ表示特征空间映射。

当SVM用于预测分析时，高维度的大型数据集会给计算带来极大的复杂性，核函数的应用能大大简化内积，从而解决维数灾难。 因此，核函数的选择（需要考虑训练样本的分布特点）是SVM预测的关键。 目前最常用的核函数有：线性核函数、高斯核函数（RBF）和多项式核函数等。 其中， RBF具有广泛的适应性，能够应用于训练样本（具有适当宽度参数）的任何分布。 尽管有时会导致过拟合问题，但它仍是使用最广泛的核函数。

集成学习（Ensemble Learning）也是机器学习中最常见的算法之一。 它通过一系列学习器进行学习，并使用某种规则把各个学习结果进行整合，从而获得比单个学习器更好的效果。 通俗地说，就是一堆弱学习器组合成一个强学习器。 在GS领域，随机森林（Random Forest，RF）和梯度提升机（Gradient Boosting Machine，GBM）是应用较多的两种集成学习算法。

RF是一种基于决策树的集成方法，也就是包含了多个决策树的分类器。 在基因组预测中，RF同SVM一样，既可用做分类模型，也可用做回归模型。 用于分类时，注意需要事先将群体中个体按表型值的高低进行划分。 RF算法可分为以下几个步骤：

最后，RF会结合分类树或回归树的输出进行预测。 在分类中，通过计算投票数（通常使用每个决策树一票）并分配投票数最高的类别来预测未观察到的类别。 在回归中，通过对ntree输出进行求平均。

有两个影响RF模型结果的重要因素：一是每个节点随机取样的协变量数量（mtry，即SNP数目）。 构建回归树时，mtry默认为p/3（p是构建树的预测数量），构建分类树时，mtry为[图片上传失败...(image-10f518-27)] ；二是决策树的数量。 很多研究表明树并非越多越好，而且构树也是非常耗时的。 在GS应用于植物育种中，通常将RF的ntree设置在500-1000之间。

当GBM基于决策树时，就是梯度提升决策树（Gradient Boosting Decision Tree，GBDT），和RF一样，也是包含了多个决策树。 但两者又有很多不同，最大的区别在于RF是基于bagging算法，也就是说它将多个结果进行投票或简单计算均值选出最终结果。 而GBDT是基于boosting算法，它通过迭代的每一步构建弱学习器来弥补原模型的不足。 GBM通过设置不同的损失函数来处理各类学习任务。

虽然已经有不少研究尝试了将多种经典机器学习算法应用于基因组预测中，但提升的准确性仍然有限，而且比较耗时。 在无数的机器学习算法中，没有一种方法能够普遍地提高预测性，不同的应用程序及其最优方法和参数是不同的。 相比于经典的机器学习算法，深度学习（Deep Learning，DL）或许是未来应用于基因组预测更好的选择。

传统的机器学习算法如SVM，一般是浅层模型。 而深度学习除了输入和输出层，还含有多个隐藏层，模型结构的深度说明了它名字的含义。 DL的实质是通过构建具有很多隐藏层的机器学习模型和海量的训练数据，来学习更有用的特征，从而最终提升分类或预测的准确性。 DL算法的建模过程可简单分为以下三步：

在GS领域，研究较多的DL算法，包括多层感知器（Multi-layer Perceptron，MPL）、卷积神经网络（Convolutional neural network，CNN）和循环神经网络（Recurrent Neural Networks，RNN）等。

MLP是一种前馈人工神经网络（Artificial Neural Network，ANN）模型，它将输入的多个数据集映射到单一的输出数据集上。 MLP包括至少一个隐藏层，如下图2中所示，除了一个输入层和一个输出层以外，还包括了4个隐藏层，每一层都与前一层的节点相连，并赋予不同权重（w），最后通过激活函数转化，将输入映射到输出端。

CNN是一类包含卷积计算且具有深度结构的前馈神经网络，通常具有表征学习能力，能够按其阶层结构对输入信息进行平移不变分类。 CNN的隐藏层中包含卷积层（Convolutional layer）、池化层（Pooling layer）和全连接层（Fully-connected layer）三类，每一类都有不同的功能，比如卷积层的功能主要是对输入数据进行特征提取，池化层对卷积层特征提取后输出的特征图进行特征选择和信息过滤，而全连接层类似于ANN中的隐藏层，一般位于CNN隐藏层的最末端，并且只向全连接层传递信号。 CNN结构如下图3所示。

需要注意的是，深度学习不是万能的。 使用DL的前提是必须具有足够大和质量好的训练数据集，而且根据GS在动植物方面的研究表明，一些DL算法和传统的基因组预测方法相比，并没有明显的优势。 不过有一致的证据表明， DL算法能更有效地捕获非线性模式。 因此，DL能够根据不同来源的数据通过集成GS传统模型来进行辅助育种。 总之，面对将来海量的育种数据，DL的应用将显得越来越重要。

以上是GS中常见的预测模型，不同分类方式可能会有所区别。 这里再简单介绍一下上述未提及到但比较重要的方法，其中一些是上述三类方法的拓展。

再生核希尔伯特空间（Reproducing Kernel Hilbert Space，RKHS）是一种典型的半参数方法。它使用高斯核函数来拟合以下模型：

RKHS模型可采用贝叶斯框架的Gibbs抽样器，或者混合线性模型来求解。

GBLUP仍然是动植物育种中广泛应用的方法，它假定所有标记都具有相同的效应。 但在实际情况中，任何与目标性状无关的标记用来估计亲缘关系矩阵都会稀释QTL的作用。 很多研究对其进行改进，主要有几种思路：

沿用以上的思路，sBLUP(Settlement of Kinship Under Progressively Exclusive Relationship BLUP, SUPER BLUP)方法将TABLUP进一步细化为少数基因控制的性状，这样基因型关系矩阵的构建仅仅使用了与性状关联的标记。

如果要在亲缘关系矩阵中考虑群体结构带来的影响，可根据个体遗传关系的相似性将其分组，然后将压缩后的组别当做协变量，替换掉原来的个体，而组内个体的亲缘关系都是一样的。 因此在构建基因组关系矩阵时，可用组别的遗传效应值来代替个体的值，用个体对应的组来进行预测，这就是cBLUP（Compressed BLUP）。

以上思路都提到了将已验证和新发现的位点整合到模型中，这些位点从何而来？最常见来源自然是全基因组关联分析（Genome Wide Association Study, GWAS）。 GS和GWAS有着天然的联系，将GWAS的显著关联位点考虑进GS中，直接的好处是能维持多世代的预测能力，间接的好处是能增加已验证突变的数量。

下图比较了GWAS辅助基因组预测的各类方法比较。 a表示分子标记辅助选择方法（MAS），只利用了少数几个主效位点；b表示经典GS方法，利用了全部标记，且标记效应相同；c对标记按权重分配；d将显著关联标记视为固定效应；e将显著关联标记视为另一个随机效应（有其自身的kernel derived）；f将染色体划分为片段，每个片段构建的G矩阵分配为不同的随机效应。

GWAS辅助基因组预测的结果会比较复杂，单纯地考虑将关联信号纳入模型不一定都能提高准确性，具体表现应该和性状的遗传构建有关。

GS对遗传效应的估计有两种不同的策略。 一是关注估计育种值，将加性效应从父母传递给子代。 而非加性效应（如显性和上位性效应）与特定基因型相关，不能直接遗传。 当估计方差组分时，非加性效应通常和随机的环境效应一起被当成噪音处理。 另一种策略同时关注加性和非加性效应，通常用于杂种优势的探索。 杂交优势一般认为是显性和上位性效应的结果，因此，如果非加性效应很明显，而你恰好将它们忽略了，遗传估计将会产生偏差。

杂种优势利用是植物育种，尤其是水稻、玉米等主粮作物的重要研究课题。 将非加性遗传效应考虑进GS模型进行杂交种预测，也是当前基因组预测在作物育种中研究的热点之一。

当然，杂种优势效应的组成也是随性状而变化的，不同性状的基因组预测需要与鉴定杂优QTL位点结合起来。由于一般配合力GCA（加性效应的反映）和特殊配合力SCA（非加性效应的反映）可能来自不同遗传效应，所以预测杂交种F 应该分别考虑GCA和SCA。GCA模型可以基于GBLUP，重点在基因型亲缘关系矩阵构建。SCA模型有两种方法：一是将杂优SNP位点的Panel作为固定效应整合进GBLUP模型中；二是使用非线性模型，如贝叶斯和机器学习方法。据报道，对于加性模型的中低遗传力性状，机器学习和一般统计模型比较一致。但在非加性模型中，机器学习方法表现更优。

传统的GS模型往往只针对单个环境中的单个表型性状，忽略了实际情况中多性状间或多环境间的相互关系。 一些研究通过对多个性状或多个环境同时进行建模，也能提高基因组预测的准确性。 以多性状（Multi-trait，MT）模型为例，多变量模型（MultivaRIAte model，MV）可用如下公式表示：

多性状选择一般用于性状间共有某种程度的遗传构建，即在遗传上是相关的。 尤其适用于对低遗传力性状（伴随高遗传力性状相关）或者难以测量的性状。

农作物的环境条件不如动物容易控制，而且大部分性状都是数量性状，很容易受到环境影响。 多环境（Multi-environment，ME）试验发挥了重要作用，基因型与环境互作（Genotype by E nvironment，G × E）效应也是当前基因组选择关注的焦点。

除了GBLUP，多变量模型也可基于贝叶斯框架的线性回归，或者基于非线性的机器学习方法。

我们知道，基因经过转录翻译以及一系列调控后才能最终体现在表型特征上，它只能在一定程度上反映表型事件发生的潜力。 随着多组学技术的发展，整合多组学数据用于基因组预测也是目前GS研究的一个重要方向。

在植物育种中，除基因组外，转录组学和代谢组学是当前GS研究相对较多的两个组学。 转录组将基因表达量与性状进行关联预测，代谢组则将调控表型的小分子含量与性状进行关联预测，对于某些特定的性状而言，可能会提高预测能力。 最好的方法是将各个组学的数据共同整合进模型，但这样会大大增加模型的复杂度。

表型测定的准确性直接影响模型的构建。 对于一些复杂性状，单凭肉眼观察记录显然已不可取，而且表型调查费时费力，成本很高。 因此，高通量表型组也是GS发展的重要方向。 表型的范畴非常之广，当个体性状不可简单测量时，我们也可采用多组学数据，如蛋白组、代谢组等数据来替代。

考虑到成本效益问题，多组学技术在动植物育种中仍处于研究阶段，但代表了未来的应用方向。

为什么在实际生活工作中几乎没有人用微积分计算？

你好，很高兴回答你的提问。 微积分在生活工作中有些专业可能还是会用到微积分计算的 ，例如理工科有很多专业都会用到微积分迭代公式，只不过有些是编辑到计算机的程序里面，可能没注意到，像土木专业、水利专业、桥梁专业、机械专业，电气、金融专业很多理工科在进行计算的时候经常都是运用到微积分理论的。 微积分是一个很强大的计算理论。 我们一般说到微积分的时候，涵盖了导数与微分，函数以及不定积分三大板块。 每个板块又细分若干个分支。 我们在求解一些复杂问题的时候，多需要用到微积分的理论，而且一般情况下都要借助计算机来模拟计算，因为复杂的计算式，通过手算很难满足迭代的关系，求解出对应的数值，我是一个做结构分析的，我们在求解计算的时候都是用的微积分理论来求解结果的。 在金融学科里面，微积分有着非常广泛的应用背景， 在数值分析过程中，微积分的作用就好比筷子一样，是我们不可或缺的必要工具，通过函数分析，分析出高点低点，研究抛物线，这些都是基于微积分理论， 其实随着科学的不断进步，我们越来越多的依靠计算机软件，所以很多复杂的理论都编程到计算软件工具里面了，这就是体现其重要性的一个很大的依据。 在整个学习环节中，数学有着举足轻重的作用，覆盖了诸多学科，而随着学习的不断深入，在研究理论加深的同时，越来越多的理论都是需要用微积分来支持，研究生、博士更是需要很好地微积分基础，帮我们解决理论上的难题， 所以微积分的用处还是很多，只不过是我们很多时候忽视了。 希望我的回答能够帮助到你。 在实际生活和工作中，绝大多数人，包括学过微积分的高学历人士，都没有直接用到微积分进行计算，这个是事实。 但是，又不能因为这个事实就认为学习微积分没有用处。 微积分对多数人来说，都比较有难度，但是，它仍然归属于基础学科。 基础，意思就 是它是为其他学科提供理论支持的，本身并不能太多用来直接去解决现实问题 。 这有点类似于高楼大厦的地基。 它们在地下，看不见摸不着，很少被提及，以致于普通人根本没有意识到它们的存在。 同样，技术密集型的工作，大家平时使用的都是专业知识和专业技术，很少提到和用到微积分，但是不能否定微积分的基础作用。 也就是说，一个人没有微积分的基础，讨论这些专业东西，那就是空中楼阁。 一个初学微积分的人，会觉得这些知识就是一些数学 游戏 ，完全看不到有什么实际用处。 但是到了更高年级，就能体会到它的作用了。 拿我比较了解的机械专业来说。 只有具备了扎实的高等数学(以微积分为主)基础，才可能学好大学物理和理论力学。 如果完全不懂微积分，那学习理论力学简直就是寸步难行。 学好了理论力学，才可能学好材料力学。 如果材料力学都没有学好，则学习机械原理就是看天书。 机械原理又是机械设计的基础。 在毕业从事专业工作时，很少用到微积分，但是大量用到机械设计。 看到没有，一环扣一环，随便缺一环都会严重影响后面的学习。 微积分最终也就成了机械设计的间接基础。 其他很多学科，特别是理工科，也是类似的道理。 在工程实践中，最后的知识形式，数学方面也就以中小学数学为主，甚至最终变成了大与小、多与少的问题。 开会或讨论时，关注的焦点也往往是值等于几，谁大谁小，而不会是一堆公式。 但是，很多专业的术语，是非常难以理解的，要理解它们那就必须曾经以扎实的数学基础，包括微积分基础，去一步一步做到的。 比方说“无功功率”，多一点好还是少一点好，到底什么意思？网络一下当然可以查到，但是如果微积分基础、电磁学基础、电工学基础不扎实，理解的也是很肤浅的。 而在工作中，一个计算(尽管没有直接用到微积分)，一个决策，往往就是比的谁理解的更透彻，要不然谁都可以做领导，做技术骨干了。 再比如现在非常火爆的人工智能，深度学习，机器学习。 深度学习的很多东西都是建立在一种叫做“随机梯度下降”的算法基础上的。 我们平时使用深度学习时，确实很少直接用到任何的微积分公式。 但是我们却不得不深刻理解什么叫随机梯度下降。 而理解它，必须有微积分基础。 你要是不信，找一个完全没有接触过微积分的人试一下，看看能理解多少。 如果理解不了，那么在实际选择深度学习算法时，会异常艰难。 因为连原理都没有搞懂，你怎么知道哪种算法更适合，参数怎么调整。 比方说：激活函数选择那一种，每一层用几个节点，总共用几层，如何避免过拟合，等等。 作出这些选择时，完全没有直接用到微积分，但是用到了“经验”，“感觉”。 这种感觉必然是建立在扎实的数学基础上的。 如果没有这种基础，那么就只是会简单套用公式(虽然都是初中生就能看懂的，除了专业术语)，而套用公式，除非别人告诉你套哪个，否则……只 有有扎实微积分、线性代数甚至概率论基础，才能深刻理解每种算法的适用范围，才能决定套哪个公式 。 微积分，以及其他一些相关的数学知识，数学思想，数学思维，已经深刻地与我们的知识结构融为一体。 回想一下，小学、初中、高中语文是不是要求背诵一大堆课文。 这么多年过去了，除了几首唐诗，试问还有几篇文章大家还能记住？我们日常生活和工作中，又用到了几篇语文的课文原文？ 但是，这些课文应该背诵吗？当然应该！这些课文，后来再也没有用到过，但是它们变成了我们后来的的字、词、句、篇的组织能力。 我们是在潜移默化中，把这些课文消化了，吸收了，最后失去了原有的形式而已。 说得更通俗一点，我们吃食物，这些食物变成了身体的一部分。 我们不能因为后来没有感觉到食物的具体形式，没有看到食物，而认为吃食物没有用。 特别地，不能感觉小时候吃的东西没有用，更不能说反正吃东西也就管一两天，“早知道以前就别吃东西了”。 微积分也是同样的道理，对于不从事研究的技术人员来说，它很少被直接应用，但不能说不该学。 它的思想已经融入到我们脑海里。 在涉及复杂设计、复杂决策时，微积分的思想就会出来帮我们。 我们只是潜意识地在做设计，做决策，已经不知道微积分帮忙的时候，到底应用了具体哪个公式、哪个定理。 这就好比说，我们长大后，可以脱口成章，可以顺口说一句成语出来，但是我们已经忘了到底小时候在哪篇课文里学到的成语。 甚至我们都不承认小时候语文学过，以为自己天生就有“语感”。 总之，除了科研人员，微积分确实很少直接用于具体计算，这是因为它是基础学科，是为专业技能提供理论支持的。 工程技术人员(建筑、施工、互联网、IT、电气电子、化工、航空航天、生物等等等等)，如果没有微积分基础，会影响实际工作中的计算和决策。 其他理工技术性不强的岗位(比如门卫、厨师、小商贩、艺术家、运动员、一线工人)，则微积分的作用小一些。 最后需要提醒一下，在日常生活中，不论是何种职业，都不需要用到微积分。 特别是大家热衷的“买菜问题”。 必须把生活和工作区分开来。 大学以后学得东西从来都不是主要用来生活的，而是用来工作的。 你好，很高兴能够回答你的问题，希望能给你带来帮助，喜欢的麻烦点个关注，谢谢大家！ 为什么在实际生活工作中几乎没有人用微积分计算？ 微积分是高等数学中研究函数的微分和积分及有关应用的数学分支。 微积分在数学，物理，化学等领域发挥着举足轻重的地位，可是，为什么很少出现在我们的实际工作中？ 我认为最大的原因是初等数学已经足够大多数工作的需要，在此基础上，没有必要再利用微积分去计算。 初等数学，包括小学时的四则运算(四则运算已经可以满足日常生活的需求），初中的时候代数几何（代数几何渐渐开始抽象，在生活中也很少应用），以及高中的时候学到的集合，基本初等函数，二次函数根分布与不等式，三角函数...等等（已经很少出现在我们的实际工作中）。 在我们工作中，很多工作岗位更侧重于效率，对精细没有过多的追求。 在生活中，更是如此。 例如：我们拿起水杯喝水，喝完水绝对不会拿起微积分把杯子中水的体积算一算。 可能会有很多人问？那为什么还要掌握微积分。 我想说的是，用不用算是一回事，会不会算是另外一回事。 而且，学习微积分并不仅仅是为了应用，更多的是可以锻炼数学的思维。 为什么在实际生活工作中几乎没有人用微积分计算？两个主要的原因就是初等数学已经足够大多数工作的需要且大部分工作岗位不必要追求精细。 但是，微积分拥有着无可替代的价值，不仅推动了数学和其他学科的发展，还推动了人类文明的进步。 你觉得呢？快来评论区评论吧。 这个问题嘛，其实反映了题主的生活层次。 很抱歉，我没有歧视的意思。 比较残酷，通常意义上 社会 的精英阶层和题主比较遥远。 作为市场卖菜、银行柜台、保安大哥、外卖小哥等职业，我当然不鼓励同学们花过多的时间学习微积分等基础数学高等应用。 但我相信，每一个父母，都不会在孩子们还在读小学一年级时，就以上述职业为终极目标，来教育孩子为此奋斗终生。 我再重申一次，我没有歧视，我只是说一个事实。 如果你觉得过于直接，我再次表示歉意。 数学专业通常被笼统地分为基础数学（Mathematics）和应用数学（Applied Mathematics）两个大项。 基础数学又称为纯粹数学，大致上是对数学结构本身的内在规律进行研究，以纯粹形式研究事物的数量关系和空间形式。 它通常包含：微分几何、数学物理、偏微分方程等。 应用数学包括两个部分，一部分就是与应用有关的数学，另外一部分是数学的其他领域应用，即以数学为工具，探讨解决科学、工程学和 社会 学方面的问题。 纯粹数学方向，就业前景比较单一，就是毕业后一般直接进入高校任职或者进入科研机构就业。 这类人在 社会 上同学们碰到的机会非常之少。 但一旦出现转业从事商业机构的情况，我们通常用一个成语形容——猛虎下山！应用数学则就业面很广了。 目前主要有两个领域。 一是计算机，一般在IT公司做数据分析、软件开发等。 二是经济学，现在的经济学有很多都需要用非常专业的数学进行分析，在精算、国际经济与贸易、化工制药、通讯工程等比较多。 随便举几个例子吧： 精算师，作为全球含金量极高的认证职业之一，精算师被Business Insider列为年度最高薪工作，我没有直接认识的精算师朋友，但在茶余饭后经常听到大神的传说，常常惊为天人！ 金融方向，在华尔街，金融数学家是最为抢手人才之一，年薪百万美元是家常便饭。 当年同校的高考状元大佬，目前就是跑美国干的这个。 IT方向，也是比较被看好的热门行业，每年的人才缺口就达数百万人，应用数学专业有其在IT行业中占据不可忽视的优势。 这个周边朋友就多些，一线城市两套房，很轻松愉快。 等等，你是不是忘记回答微积分的事情了呢？哦，对啊！ 数学专业按照难度来看，最基础的几门课程分别是：微积分、线性代数、统计学。 大家明白了吗？ 学好数理化，走遍天下都不怕！ 我是猫先生，感谢阅读！ 你是不是感觉四则运算也很少用了，有计算器，小贩都不自己算了，还学算数干嘛？但是，用着的人也很多，至少我周围的人天天在用微积分套公式。 上次做了个计算，需要好好多参数的方程，找了个郑州的公司做参数20人，干了一个月才把参数整理好，做参数都没有学过微积分，不耽误他们做微积分参数，他们说自己是做AI的。 微积分都是劳动密集型工人在用，普通人用不到了。 首先回答题主问题！ 现实生活很少利用到微积分是事实，可能会有人提部分采用了微积分计算的例子，但也不能改变微积分在大部分人的生活中不存在的现实。 原因是当我们的生活中需要采用到微积分计算就说明了这项工作对数据的精细程度是敏感的。 可能千分之一或万分之一的数据误差都会导致整个工作失败。 而我们普通人是用不到这么高的精细度，这种误差对我们普通人的生活是没有影响的。 两根筷子的半截面面积差零点一平方毫米是不影响我们夹菜的。 总结：微积分的理论价值在于告诉大家，数学上可以依靠夹逼定理来确定极限，这既是一种计算方式也是一种数学思维。 就像微观物理学中的粒子无限可分的假设一样，它对现实生活几乎毫无影响，但却是攀登高峰的必要台阶。 一个有点的故事，一个地主老爷要阿凡提修一座有二楼的漂亮楼房，但他不要一层。 不是没用过，只不过没有这个意识而已，比如饭要一口口吃，直到吃饱，这就是积分；从a地到b地，要找最短的路线，这就是梯度下降，背后就是微分的思想；从多次发生的一堆事情里得知一定的规律，并预测下一刻会发生什么，这就是回归、预测和概率....很多事情我们都下意识地做了，只不过没有进行概念上的明确，所以才以为没做。 人家说的是现实生活中很少有用微积分计算 没说微积分脱离实际应用 一个个吹的跟研究火箭上天一样 事实就是很少有人用微积分计算 主要就是大多数人接触的层面基本就是经验加手册 微积分推倒出的很多公式直接套就行 我曾经问过一个博士 我说微积分对于你是不是跟加减乘除对于我们一样 已经融入到骨子里了 他呵呵一笑 告诉我基本用不上 时间长了也都忘了 提这个问题的人应该说根本就不知道微积分。 在现实生活中，微积分到处都是，比如所谓的积分，就是乘法加累加（累积，所以叫积分），比如水费就是这样，电费也是如此，各种按天累积按月累积按年累积的都是如此，在我们生活中到处都是，更不用说比较专业的地方。 微分也是如此，微分的特点就是趋势，比如看见云越来越厚，就会感觉要下雨了，看见风越来越大，赶紧收衣服，上班早一点出去避免堵车也是微分的结果。 这些事情不一定要进行详细计算，或者计算的时候取样也不必无限小或者无限大（取极限），其结果满足生活上的需要即可，比如电费的计算，不必按秒取样，按天就足够精确了，不准确的误差可以累积到下个月，这样计算起来就非常简单，虽然这样可能会产生多个解，但是可以用生活常识或行政法规进行约束确保只有一个解，比如计算日期截止到月底就是这个意思。 其实有，只是你不会而已…… 生活中的计算并不少，微积分也有用处，但大多数人不会，自然也不会觉得自己吃亏，更不会觉得有用了。 最简单的，我们笑话里经常说的买披萨，12寸没有了，给你换两个8寸的行不行？这其实就是数学知识，你不会，被骗了还美滋滋。 更难一点的。 数学家王元和妻子买西瓜，大西瓜是小西瓜价格的三倍。 王元就和妻子争论到底买哪种，王元认为大西瓜半径大一半，那体积大3倍多一点，妻子认为大西瓜瓜皮也厚，王元又认为三个小瓜的比一个大瓜的皮还多…… 你看，其实生活中的数学问题真不少见，我们其实每时每刻都在做数学问题，遇到很多选择，其实你都是在做概率问题，只是你自己都不会意识到。 遇到两条路，你的第一反应肯定是想想哪一条近的概率更大。 所以我还是这个观点，一门学科有没有用，不是学科本身决定的，而是掌握学科的人决定的。 一个不会英语的人永远也不会想着看英文书，同样一个不会数学的人同样也不会想用数学去解决问题，因为他们根本意识不到这是数学问题！

高层拟合是什么意思？

高层拟合是指在机器学习中，利用大规模数据对模型进行训练，在保证模型符合业务需求的前提下，实现模型对数据的高度拟合能力。 高层拟合通常需要具备大量的计算资源和高效的算法，以处理多维、非线性、复杂的数据结构。 高层拟合的实现，可以提高模型的精度和准确性，提升业务决策的可靠性和效率，具有重要的应用价值。 在大数据时代，高层拟合已经成为机器学习领域的研究热点之一。 高层拟合的实现需要综合考虑数据质量、特征工程、模型选择、超参数调整等多方面因素。 同时，为了进一步提高模型的泛化能力和鲁棒性，需要使用交叉验证等技术进行模型评估。 高层拟合的研究，涉及到数据挖掘、人工智能、计算机视觉等多个领域，涵盖了从理论研究到工程实践的全过程。 高层拟合虽然在机器学习中有着广泛的应用，但同时也存在着一系列问题和挑战。 例如，模型的复杂度可能过高，出现过拟合等问题；或者模型的泛化能力不足，存在欠拟合的情况。 因此，如何兼顾模型的复杂度和泛化能力，对于高层拟合具有重要的意义。 另外，在一些领域，如医疗、金融等，由于数据集数量有限，高层拟合的实现受到一定限制。 因此，需要在实践中不断探索和创新，以满足不同领域的业务需求。

多项式曲线拟合

多项式曲线拟合：深度解析与实战

在机器学习的世界里，多项式拟合犹如一柄精妙的工具，其应用广泛而深入。 让我们通过一个生动的实例，借助Python的强大库——, numpy, sklearn(包括LinearRegression, Ridge, PolynomialFeatures)，来探索其魔力。 设想我们手头有一组训练数据，这些数据是均匀分布在区间[0,1]的观测值，再附加了些随机噪声，我们的目标是通过多项式拟合逼近目标函数——那个神秘的$\sin(2\pi x)$。 绿色曲线就是它的身影，而我们的任务则是用线性对系数的多项式来逼近，误差衡量标准则是均方误差。

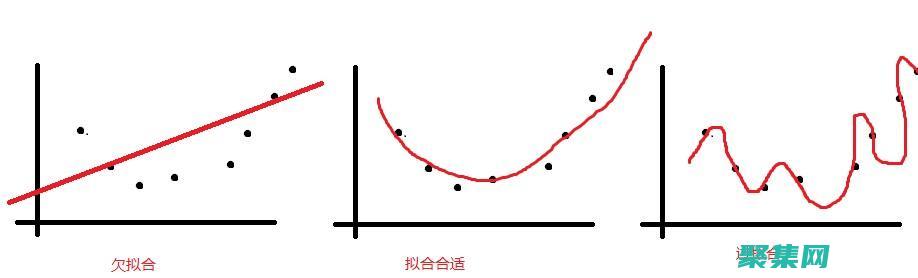
当我们将多项式拟合的阶数分别设为0, 1, 3, 9，你会发现它们之间的差异犹如夜与昼。 特别是当阶数提升到较高水平，比如9阶时，拟合效果可能会显得力不从心，甚至适得其反，这就是欠拟合与过拟合的微妙之处。 过拟合就像一个过于复杂的舞者，过于关注细节而忽略了整体的韵律，对噪声过于敏感，导致在测试数据上表现不佳。

如何避免过拟合？正则化是我们的解药。 例如，通过Ridge Regression，我们可以调整多项式系数的复杂度，引入λ参数来平衡模型的简洁性和拟合精度。 当λ值适当时，模型既能抓住数据的主要趋势，又能有效抵抗噪声的影响。 关键在于找到那个微妙的平衡点，让模型既不过度拟合又不会欠拟合。

在这个过程中，我们不仅要关注模型的复杂度，还要增大数据规模，提供更多样化的样本，以提高模型的泛化能力。 理论与实践并重，参考《Pattern Recognition and Machine Learning》(PRML)和《Python Machine Learning》(PyMachine)，你会发现每一次尝试和调整都是对知识的深化和理解的提升。

通过以上讲解，你对多项式拟合有了更深入的认识，它既是机器学习中的基础工具，也是提升模型性能的智慧钥匙。让我们继续探索这个富有挑战与乐趣的领域吧！

---

---

相关标签： 多项式拟合在线、 多项式拟合在机器学习和人工智能中的应用、 从理论到实践、

上一篇：使用polyfit应对复杂数据高级建模技术和故

下一篇：超越polyfit探索多项式回归的替代方法和扩