人生苦短

网站标签

Python、 Python博客、 Python、 Blog、 PHP、 LAMP、

---

网站描述

人生苦短，我爱Coding...

---

上一篇：共享充电宝软件开发定制公司平台-智能硬件软件系统方案-电动自行单车充电桩-云上智诚

下一篇：首页-信息安全、数据安全、应用安全、私有云、数据中心、虚拟

seo综合信息

SEO信息	百度来访IP：- | 移动端来访IP：- | 出站链接：0 | 站内链接：0
IP网速：	IP地址：114.215.114.30 [中国山东青岛 阿里云] | 网速：104毫秒
ALEXA排名	世界排名：- | 预估IP：- | 预估PV：-
备案信息	登录可见 | 名称：登录可见 | 已创建：9年7个月5天

收录	百度	360	搜狗	谷歌
查询	0	0	0	0

电脑关键词	手机关键词	页面友好	首页位置	索引	近期收录
0	0	电脑端优秀	-	0	0

协议类型HTTP/1.1 200 OK 页面类型text/html; charset=UTF-8 服务器类型Apache/2.2.22 (Ubuntu) 是否压缩是 原网页大小55760 压缩后大小18343 压缩比67.1%

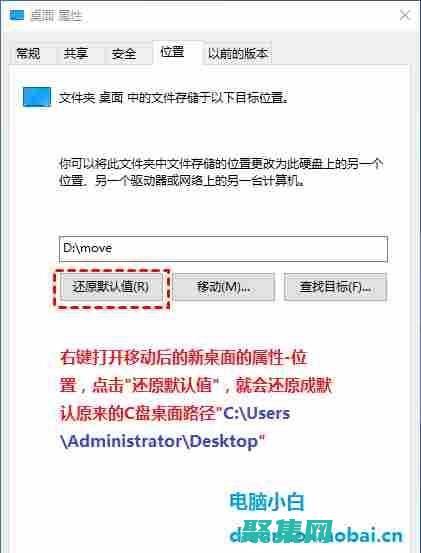
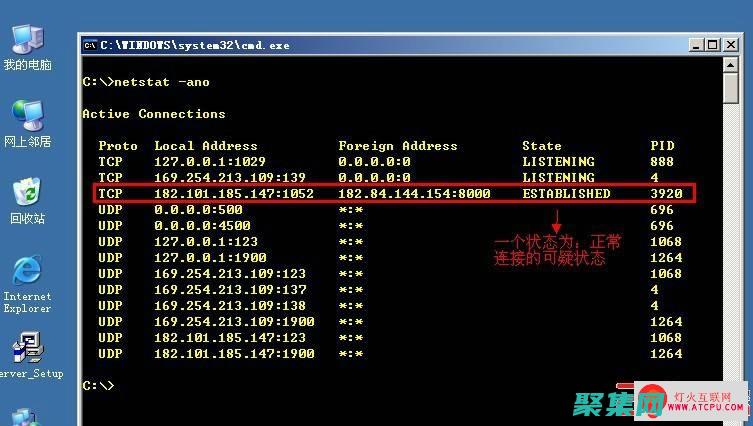
网站快照

人 生 苦 短 当 前 网 页 不 支 持 你 正 在 使 用 的 浏 览 器 . 为 了 正 常 的 访 问 , 请 升 级 你 的 浏 览 器 . 人 生 苦 短 人 生 苦 短 ， 我 爱 C o d i n g . . . 搜 索 关 键 字 搜 索 首 页 关 于 配 置 文 件 用 H O C O N / . c o n f 还 是 j s o n 作 者 : 曹 容 端 时 间 : 2 0 2 0 0 7 2 2 分 类 : P y t h o n 评 论 简 单 比 较 一 下 两 种 配 置 文 件 的 优 缺 点 ： J S O N : e a s y t o g e n e r a t e p r o g r a m m a t i c a l l y w e l l d e f i n e d a n d s t a n d a r d b a d f o r h u m a n m a i n t e n a n c e , w i t h n o w a y t o w r i t e c o m m e n t s , a n d n o m e c h a n i s m s t o a v o i d d u p l i c a t i o n o f s i m i l a r c o n f i g s e c t i o n s c o n f n i c e f o r h u m a n s t o r e a d , t y p e , a n d m a i n t a i n , w i t h m o r e l e n i e n t s y n t a x b u i l t i n t o o l s t o a v o i d c u t a n d p a s t e w a y s t o r e f e r t o t h e s y s t e m e n v i r o n m e n t , s u c h a s s y s t e m p r o p e r t i e s a n d e n v i r o n m e n t v a r i a b l e s T h e i d e a w o u l d b e t o u s e J S O N i f y o u r e w r i t i n g a s c r i p t t o s p i t o u t c o n f i g , a n d u s e H O C O N i f y o u r e m a i n t a i n i n g c o n f i g b y h a n d . I f y o u r e d o i n g b o t h , t h e n m i x t h e t w o . 简 单 比 较 一 下 两 种 配 置 文 件 的 优 缺 点 ： J S O N : e a s y t o g e n e r a t e p r o g r a m m a t i c a l l y w e l l d e f i n e d a n d s t a n d a r d b a d f o r h u m a n m a i n t e n a n c e , w i t h n o w a y t o w r i t e c o m m e n t s , a n d n o m e c h a n i s m s t o a v o i d d u p l i c a t . . . P y t h o n R e c o r d s 库 使 用 详 解 作 者 : 曹 容 端 时 间 : 2 0 1 9 0 9 0 1 分 类 : P y t h o n 5 条 评 论 R e c o r d s 是 K e n n e t h R e i t z f o r H u m a n s ™ 系 列 继 r e q u e s t s 后 的 又 一 大 作 ， 官 方 描 述 为 只 需 编 写 S Q L ， 其 他 交 给 R e c o r d s ， 它 使 得 工 作 流 程 尽 可 能 简 单 ， 同 时 提 供 一 个 优 雅 的 方 式 处 理 查 询 结 果 。 官 方 网 站 ： h t t p s : / / g i t h u b . c o m / k e n n e t h r e i t z / r e c o r d s 2 0 1 9 年 1 0 月 2 1 日 更 新 ： 在 目 前 的 版 本 中 存 在 一 个 b u g ： 当 使 用 S Q L i t e 实 体 数 据 库 而 非 内 存 数 据 库 的 时 候 ， 会 报 如 下 错 误 ： s q l a l c h e m y . e x c . P r o g r a m m i n g E r r o r : ( s q l i t e 3 . P r o g r a m m i n g E r r o r ) C a n n o t o p e r a t e o n a c l o s e d d a t a b a s e . b u g i s s u e s 1 2 8 : h t t p s : / / g i t h u b . c o m / k e n n e t h r e i t z / r e c o r d s / i s s u e s / 1 2 8 原 因 可 能 是 ： 当 我 们 执 行 操 作 的 时 候 ， c u r s o r 可 能 已 经 关 闭 。 目 前 g d t r o s z a k 已 经 在 分 支 c o n n e c t i o n f i x r e d u x 中 修 复 了 这 个 b u g 连 接 数 据 库 > > > i m p o r t r e c o r d s > > > d b = r e c o r d s . D a t a b a s e ( s q l i t e : / / / t e s t . d b ) R e c o r d s 使 用 s q l a l c h e m y 的 c r e a t e _ e n g i n e ， D B A P I 可 以 完 全 参 照 s q l a l c h e m y 文 档 ， 如 下 示 例 列 出 了 连 接 P o s t g r e S Q L ， M y S Q L ， O r a c l e ， M i c r o s o f t S Q L S e r v e r ， S Q L i t e 的 D B A P I ： 注 ： D B A P I 是 符 合 R F C 1 7 3 8 U n i f o r m R e s o u r c e L o c a t o r s ( U R L ) 定 义 的 一 种 数 据 库 连 接 方 式 P o s t g r e S Q L # d e f a u l t d b = r e c o r d s . D a t a b a s e ( p o s t g r e s q l : / / s c o t t : t i g e r @ l o c a l h o s t / m y d a t a b a s e ) # p s y c o p g 2 d b = r e c o r d s . D a t a b a s e ( p o s t g r e s q l + p s y c o p g 2 : / / s c o t t : t i g e r @ l o c a l h o s t / m y d a t a b a s e ) # p g 8 0 0 0 d b = r e c o r d s . D a t a b a s e ( p o s t g r e s q l + p g 8 0 0 0 : / / s c o t t : t i g e r @ l o c a l h o s t / m y d a t a b a s e ) M y S Q L # d e f a u l t d b = r e c o r d s . D a t a b a s e ( m y s q l : / / s c o t t : t i g e r @ l o c a l h o s t / f o o ) # m y s q l c l i e n t ( a m a i n t a i n e d f o r k o f M y S Q L P y t h o n ) d b = r e c o r d s . D a t a b a s e ( m y s q l + m y s q l d b : / / s c o t t : t i g e r @ l o c a l h o s t / f o o ) # P y M y S Q L d b = r e c o r d s . D a t a b a s e ( m y s q l + p y m y s q l : / / s c o t t : t i g e r @ l o c a l h o s t / f o o ) O r a c l e d b = r e c o r d s . D a t a b a s e ( o r a c l e : / / s c o t t : t i g e r @ 1 2 7 . 0 . 0 . 1 : 1 5 2 1 / s i d n a m e ) d b = r e c o r d s . D a t a b a s e ( o r a c l e + c x _ o r a c l e : / / s c o t t : t i g e r @ t n s n a m e ) M i c r o s o f t S Q L S e r v e r # p y o d b c d b = r e c o r d s . D a t a b a s e ( m s s q l + p y o d b c : / / s c o t t : t i g e r @ m y d s n ) # p y m s s q l d b = r e c o r d s . D a t a b a s e ( m s s q l + p y m s s q l : / / s c o t t : t i g e r @ h o s t n a m e : p o r t / d b n a m e ) S Q L i t e # f o r a r e l a t i v e f i l e p a t h d b = r e c o r d s . D a t a b a s e ( s q l i t e : / / / f o o . d b ) # f o r a a b s o l u t e f i l e p a t h # U N I X / M A C d b = r e c o r d s . D a t a b a s e ( s q l i t e : / / / / a b s o l u t e / p a t h / t o / f o o . d b ) # W i n d o w s d b = r e c o r d s . D a t a b a s e ( s q l i t e : / / / C : \ \ \ \ p a t h \ \ \ \ t o \ \ \ \ f o o . d b ) # W i n d o w s u s i n g r a w s t r i n g d b = r e c o r d s . D a t a b a s e ( r s q l i t e : / / / C : \ \ p a t h \ \ t o \ \ f o o . d b ) # f o r a m e m o r y d a t a b a s e d b = r e c o r d s . D a t a b a s e ( s q l i t e : / / ) 查 询 R e c o r d s 可 以 方 便 的 使 用 S Q L 语 句 来 查 询 数 据 ， 通 过 调 用 q u e r y 方 法 ， 对 返 回 的 结 果 ， 我 们 无 需 过 多 处 理 ， 就 可 以 方 便 的 使 用 。 > > > r o w s = d b . q u e r y ( S E L E C T * F R O M u s e r s ) 对 于 查 询 语 句 来 说 ， R e c o r d s 返 回 的 是 一 个 R e c o r d 对 象 或 R e c o r d 对 象 的 一 个 列 表 。 我 们 可 以 调 用 R e c o r d 对 象 内 置 方 法 ， 比 如 ： a s _ d i c t ( ) 作 为 一 个 字 典 返 回 。 a s _ d i c t ( o r d e r e d = T r u e ) 作 为 一 个 O r d e r e d D i c t 返 回 。 我 们 还 可 以 像 操 作 字 典 一 样 去 操 作 R e c o r d 对 象 ， 比 如 使 用 k e y s ( ) 和 v a l u e s ( ) # 处 理 单 条 数 据 > > > r o w s [ 0 ] > > > r o w s [ 0 ] . a s _ d i c t ( ) > > > r o w s [ 0 ] . n a m e 张 三 > > > r o w s [ 0 ] . g e t ( c i t y ) 南 京 # 处 理 多 条 数 据 > > > r o w s . a l l ( ) [ , , , ] > > > r o w s . a s _ d i c t ( ) [ , , , ] 我 们 也 可 以 像 处 理 任 何 可 迭 代 对 象 一 样 使 用 循 环 来 遍 历 每 一 行 数 据 。 # 循 环 数 据 集 > > > f o r r o w i n r o w s : p r i n t ( r o w . n a m e , r o w . c i t y ) 张 三 南 京 李 四 深 圳 王 五 上 海 张 三 北 京 R e c o r d s 使 用 t a b l i b 来 处 理 数 据 导 出 ， t a b l i b 是 一 个 纯 P y t h o n 编 写 的 格 式 无 关 的 表 格 数 据 处 理 库 ， 使 用 t a b l i b 我 们 可 以 方 便 的 将 R e c o r d s 对 象 导 出 成 下 列 格 式 ： E x c e l ( S e t s + B o o k s ) J S O N ( S e t s + B o o k s ) Y A M L ( S e t s + B o o k s ) P a n d a s D a t a F r a m e s ( S e t s ) H T M L ( S e t s ) J i r a ( S e t s ) T S V ( S e t s ) O D S ( S e t s ) C S V ( S e t s ) D B F ( S e t s ) 在 R e c o r d s 类 中 ， 内 置 了 一 个 d a t a s e t 属 性 ， 用 来 生 成 一 个 t a b l i b 的 D a t a s e t 对 象 ， 也 提 供 了 一 个 e x p o r t 方 法 ， 可 以 将 D a t a s e t 对 象 转 化 为 我 们 所 需 要 的 格 式 ： > > > p r i n t ( r o w s . d a t a s e t ) i d | n a m e | a g e | c i t y | | | 1 | 张 三 | 2 7 | 南 京 2 | 李 四 | 3 2 | 深 圳 3 | 王 五 | 2 7 | 上 海 4 | 张 三 | 2 7 | 北 京 > > > r o w s . e x p o r t ( j s o n ) [ , , , ] > > > p r i n t ( r o w s . e x p o r t ( t s v ) ) i d n a m e a g e c i t y 1 张 三 2 7 南 京 2 李 四 3 2 深 圳 3 王 五 2 7 上 海 4 张 三 2 7 北 京 x l s , x l s x , d b f , o d s 这 类 二 进 制 数 据 ， 可 以 直 接 保 存 成 文 件 > > > w i t h o p e n ( o u t p u t . x l s , w b ) a s f : f . w r i t e ( r o w s . e x p o r t ( x l s ) ) 命 令 行 工 具 R e c o r d s 还 提 供 了 一 个 命 令 行 工 具 ， 方 便 的 在 终 端 使 用 ： u s e a g e : r e c o r d s [ ] [ . . . ] [ u r l = ] r e c o r d s h > > > r e c o r d s s e l e c t * f r o m u s e r s t s v u r l s q l i t e : / / / t e s t . d b i d n a m e a g e c i t y 1 张 三 2 7 南 京 2 李 四 3 2 深 圳 3 王 五 2 7 上 海 4 张 三 2 7 北 京 其 他 操 作 正 如 官 方 的 s l o g a n 一 样 ： R e c o r d s : S Q L f o r H u m a n s ™ ， R e c o r d s 是 一 个 非 常 简 单 ， 但 是 很 强 大 的 ， 使 用 原 生 的 S Q L 语 句 来 处 理 大 部 分 的 关 系 型 数 据 库 的 操 作 。 # I N S E R T d b . q u e r y ( I N S E R T I N T O u s e r s ( n a m e , a g e , c i t y ) V A L U E S ( : n a m e , : a g e , : c i t y ) , n a m e = n a m e , a g e = a g e , c i t y = c i t y ) # U P D A T E d b . q u e r y ( U P D A T E u s e r s S E T c i t y = 成 都 W H E R E n a m e = 赵 六 ) # D E L E T E d b . q u e r y ( D E L E T E F R O M u s e r s W H E R E n a m e = 赵 六 ) 版 权 声 明 © 著 作 权 归 作 者 所 有 允 许 自 由 转 载 ， 但 请 保 持 署 名 和 原 文 链 接 。 不 允 许 商 业 用 途 、 盈 利 行 为 及 衍 生 盈 利 行 为 。 参 考 文 档 r e c o r d s 官 方 网 站 s q l a l c h e m y 官 方 文 档 c r e a t e _ e n g i n e t a b l i b 官 方 网 站 p y t h o n r e c o r d s 使 用 方 法 R e c o r d s 是 K e n n e t h R e i t z f o r H u m a n s ™ 系 列 继 r e q u e s t s 后 的 又 一 大 作 ， 官 方 描 述 为 只 需 编 写 S Q L ， 其 他 交 给 R e c o r d s ， 它 使 得 工 作 流 程 尽 可 能 简 单 ， 同 时 提 供 一 个 优 雅 的 方 式 处 理 查 询 结 果 。 官 方 网 站 ： h t t p s : / / g i t h u b . c o m / k e n n e t h r e i t z / r e c o r d s 2 0 1 9 年 1 0 月 2 1 日 更 新 ： 在 . . . 工 作 量 证 明 之 H a s h c a s h 算 法 ， 了 解 一 下 ？ 作 者 : 曹 容 端 时 间 : 2 0 1 8 1 1 2 6 分 类 : A l g o r i t h m 5 条 评 论 图 片 来 源 于 网 络 一 、 基 础 概 念 H a s h c a s h 是 一 个 工 作 量 证 明 （ p r o o f o f w o r k ） 算 法 ， 可 以 用 于 垃 圾 邮 件 过 滤 ， 拒 绝 服 务 攻 击 （ D D O S ） 等 领 域 。 比 特 币 中 挖 矿 算 法 的 工 作 量 证 明 机 制 也 是 基 于 H a s h c a s h 来 实 现 的 。 H a s h c a s h 由 A d a m B a c k 于 1 9 9 7 年 首 次 提 出 ， 论 文 戳 这 里 。 先 来 了 解 一 下 H a s h c a s h 算 法 的 原 理 吧 。 正 如 密 码 学 中 的 数 学 问 题 — — 难 于 解 答 ， 易 于 校 验 ， h a s h c a s h 算 法 的 设 计 灵 感 也 是 来 源 于 此 ： 要 求 用 户 计 算 一 个 中 等 难 度 但 不 难 解 决 的 功 能 ， 以 便 获 得 对 资 源 的 访 问 权 限 ， 从 而 防 止 轻 率 使 用 。 在 垃 圾 邮 件 和 D D O S 中 ， 攻 击 方 几 乎 是 没 有 代 价 的 。 垃 圾 邮 件 软 件 可 以 批 量 、 高 并 发 的 发 送 邮 件 给 目 标 地 址 ； D D O S 可 以 利 用 海 量 的 肉 鸡 对 目 标 主 机 进 行 网 络 请 求 从 而 使 目 标 主 机 限 于 瘫 痪 。 H a s h c a s h 解 决 这 些 问 题 的 手 段 是 让 攻 击 方 付 出 一 些 计 算 资 源 的 「 代 价 」 。 首 先 ， 目 标 方 会 按 照 既 定 规 则 给 出 一 道 数 学 题 ， 这 道 数 学 题 的 结 果 不 可 复 用 （ 每 次 请 求 需 要 重 新 计 算 ） 。 为 了 得 出 结 果 ， 需 要 一 些 C P U 的 计 算 资 源 ， 然 后 把 计 算 结 果 附 在 请 求 上 提 交 给 目 标 方 ， 目 标 方 可 以 非 常 轻 易 的 验 证 结 果 是 否 正 确 。 这 道 数 学 题 的 难 度 可 以 定 义 。 具 体 来 说 ， h a s h c a s h 是 基 于 h a s h 的 ， 在 通 常 情 况 下 ， 使 用 的 是 s h a 算 法 。 拿 电 子 邮 件 举 例 ， 我 要 求 所 有 发 给 我 的 电 子 邮 件 h e a d e r 中 必 须 包 含 一 个 合 法 的 「 戳 记 」 。 这 个 戳 记 中 包 含 着 一 个 特 定 的 比 特 值 和 我 的 电 子 邮 件 地 址 以 及 一 个 计 数 器 等 等 一 系 列 信 息 。 比 如 一 个 戳 记 的 比 特 值 是 2 0 ， 那 么 我 要 求 通 过 这 个 戳 记 生 成 的 哈 希 值 的 前 面 2 0 个 比 特 位 都 是 零 。 这 样 的 戳 记 我 认 为 是 合 法 的 。 为 了 得 到 这 个 戳 记 ， 算 法 会 不 断 的 累 加 计 数 器 进 行 h a s h 碰 撞 ， 在 进 行 了 上 百 万 次 的 计 算 后 ， 终 于 得 到 了 2 0 个 比 特 位 的 前 导 零 。 对 于 目 前 的 主 流 电 脑 来 说 ， 百 万 次 h a s h 大 概 需 要 几 秒 钟 时 间 。 我 相 信 ， 如 果 你 很 有 诚 意 发 送 一 个 邮 件 给 我 ， 应 该 不 会 在 乎 这 几 秒 钟 。 但 是 ， 对 于 垃 圾 邮 件 软 件 和 D D O S 来 说 ， 每 个 请 求 的 计 算 累 加 却 是 及 其 昂 贵 的 ， 难 以 实 现 批 量 的 、 大 规 模 的 网 络 请 求 。 你 看 ， 让 你 每 次 作 恶 付 出 有 限 的 一 些 成 本 ， 而 当 你 需 要 批 量 作 恶 的 时 候 ， 累 加 的 高 昂 成 本 会 使 你 望 而 却 步 。 来 具 体 看 看 h a s h c a s h 戳 记 是 长 这 个 样 子 的 ， 通 常 包 含 七 个 域 ， 每 个 域 使 用 : 分 割 。 1 : b i t s : d a t e : r e s o u r c e : e x t : s a l t : s u f f i x 七 个 域 说 明 如 下 ： 1 . 版 本 号 （ 版 本 0 更 简 单 ， 但 是 有 一 些 局 限 性 ） 。 2 . 声 明 的 比 特 值 。 如 果 戳 记 没 有 真 正 地 使 用 声 明 的 前 导 零 比 特 进 行 散 列 ， 那 么 它 就 是 非 法 的 。 3 . 生 成 戳 记 的 日 期 （ 和 时 间 ） 。 可 以 认 为 当 前 时 间 之 后 的 戳 记 以 及 那 些 在 很 久 以 前 的 戳 记 是 非 法 的 。 4 . 戳 记 为 哪 个 资 源 而 生 成 。 可 能 是 一 个 电 子 邮 件 地 址 ， 但 是 也 可 能 是 一 个 U R I 或 者 其 他 命 名 的 资 源 。 5 . 特 定 应 用 程 序 可 能 需 要 的 扩 展 。 任 何 附 加 的 数 据 都 可 以 放 置 在 这 里 ， 但 是 ， 在 到 目 前 为 止 的 使 用 中 ， 这 个 域 通 常 是 空 的 。 6 . 将 该 戳 记 与 其 他 所 有 人 为 相 同 的 资 源 在 同 一 日 期 生 成 的 戳 记 区 别 开 来 的 随 机 因 子 （ s a l t ） 。 例 如 ， 两 个 不 同 的 人 可 以 合 情 合 理 地 在 同 一 天 向 我 的 同 一 个 地 址 发 送 电 子 邮 件 。 他 们 不 应 该 由 于 我 使 用 了 d o u b l e s p e n d 数 据 库 而 无 法 发 送 成 功 。 但 是 ， 如 果 他 们 每 个 人 都 使 用 一 个 随 机 因 子 ， 那 么 完 整 戳 记 将 是 不 同 的 。 7 . 后 缀 是 算 法 真 正 起 作 用 的 部 分 。 假 定 给 出 了 前 6 个 域 ， 为 了 生 成 一 个 通 过 期 望 数 目 的 前 导 零 进 行 散 列 的 的 戳 记 ， m i n t e r 必 须 尝 试 很 多 连 续 的 后 缀 值 。 e g . # 2 0 比 特 位 h a s h c a s h ， 一 个 十 六 进 制 字 符 代 表 4 个 比 特 位 # 耗 时 1 0 . 5 2 8 3 4 2 9 6 2 3 秒 ， 计 算 2 2 3 0 4 2 7 次 1 : 2 0 : 1 8 1 1 2 6 : f o o : : + J B v h r p i : 2 2 0 8 9 b 0 0 0 0 0 b a 4 5 b 8 0 5 9 9 e 9 8 4 9 a 7 8 7 7 9 8 3 1 2 d c 7 5 3 3 c 7 e d 二 、 代 码 实 现 这 里 是 D a v i d M e r t z , P h . D . 实 现 的 P y t h o n 版 本 的 h a s h c a s h i m p o r t s y s f r o m s t r i n g i m p o r t a s c i i _ l e t t e r s f r o m m a t h i m p o r t c e i l , f l o o r f r o m s h a i m p o r t s h a f r o m r a n d o m i m p o r t c h o i c e f r o m t i m e i m p o r t s t r f t i m e , l o c a l t i m e , t i m e E R R = s y s . s t d e r r # D e s t i n a t i o n f o r e r r o r m e s s a g e s D A Y S = 6 0 * 6 0 * 2 4 # S e c o n d s i n a d a y t r i e s = [ 0 ] # C o u n t h a s h e s p e r f o r m e d f o r b e n c h m a r k d e f m i n t ( r e s o u r c e , b i t s = 2 0 , n o w = N o n e , e x t = , s a l t c h a r s = 8 , s t a m p _ s e c o n d s = F a l s e ) : # 挖 掘 一 个 新 的 h a s h ， 满 足 前 导 零 为 b i t s 位 # # r e s o u r c e : 资 源 ， 在 垃 圾 邮 件 过 滤 中 ， 通 常 表 示 邮 箱 地 址 # b i t s : 比 特 位 ， 默 认 2 0 ， 表 示 h a s h 前 5 为 是 零 （ 十 六 进 制 每 字 符 4 比 特 位 ） # n o w : 日 期 # e x t : 扩 展 字 段 ， 通 常 留 空 # s a l t c h a r s : 盐 的 长 度 # s t a m p _ s e c o n d s : n o w 字 段 是 否 支 持 秒 级 别 # v e r = 1 n o w = n o w o r t i m e ( ) i f s t a m p _ s e c o n d s : t s = s t r f t i m e ( % y % m % d % H % M % S , l o c a l t i m e ( n o w ) ) e l s e : t s = s t r f t i m e ( % y % m % d , l o c a l t i m e ( n o w ) ) c h a l l e n g e = % s : * 6 % ( v e r , b i t s , t s , r e s o u r c e , e x t , _ s a l t ( s a l t c h a r s ) ) r e t u r n c h a l l e n g e + _ m i n t ( c h a l l e n g e , b i t s ) d e f _ s a l t ( l ) : # 返 回 一 个 l 长 度 的 随 机 字 符 串 a l p h a b e t = a s c i i _ l e t t e r s + + / = r e t u r n . j o i n ( [ c h o i c e ( a l p h a b e t ) f o r _ i n [ N o n e ] * l ] ) d e f _ m i n t ( c h a l l e n g e , b i t s ) : # 部 分 h a s h 碰 撞 c o u n t e r = 0 h e x _ d i g i t s = i n t ( c e i l ( b i t s / 4 . ) ) z e r o s = 0 * h e x _ d i g i t s w h i l e 1 : d i g e s t = s h a ( c h a l l e n g e + h e x ( c o u n t e r ) [ 2 : ] ) . h e x d i g e s t ( ) i f d i g e s t [ : h e x _ d i g i t s ] = = z e r o s : t r i e s [ 0 ] = c o u n t e r r e t u r n h e x ( c o u n t e r ) [ 2 : ] c o u n t e r + = 1 d e f c h e c k ( s t a m p , r e s o u r c e = N o n e , b i t s = N o n e , c h e c k _ e x p i r a t i o n = N o n e , d s _ c a l l b a c k = N o n e ) : # 校 验 s t a m p 是 否 合 法 # # 如 果 指 定 了 c h a c k _ e x p i r a t i o n （ 应 该 用 数 字 来 表 示 ） ， 表 示 有 效 期 # > > > f r o m h a s h c a s h i m p o r t D A Y S # > > > c h e c k ( s t a m p , c h e c k _ e x p i r a t i o n = 2 8 * D A Y S ) # i f s t a m p . s t a r t s w i t h ( 0 : ) : # V e r s i o n 0 t r y : d a t e , r e s , s u f f i x = s t a m p [ 2 : ] . s p l i t ( : ) e x c e p t V a l u e E r r o r : E R R . w r i t e ( M a l f o r m e d v e r s i o n 0 h a s h c a s h s t a m p ! \ \ n ) r e t u r n F a l s e i f r e s o u r c e i s n o t N o n e a n d r e s o u r c e ! = r e s : r e t u r n F a l s e e l i f c h e c k _ e x p i r a t i o n i s n o t N o n e : g o o d _ u n t i l = s t r f t i m e ( % y % m % d % H % M % S , l o c a l t i m e ( t i m e ( ) c h e c k _ e x p i r a t i o n ) ) i f d a t e i n t ( c l a i m ) : r e t u r n F a l s e e l i f c h e c k _ e x p i r a t i o n i s n o t N o n e : g o o d _ u n t i l = s t r f t i m e ( % y % m % d % H % M % S , l o c a l t i m e ( t i m e ( ) c h e c k _ e x p i r a t i o n ) ) i f d a t e > > > f r o m h a s h c a s h i m p o r t m i n t , _ m i n t > > > m i n t ( f o o , b i t s = 1 6 ) 1 : 1 6 : 0 4 0 9 2 2 : f o o : : + A r S r t K d : 1 6 4 b 3 > > > _ m i n t ( f o o , b i t s = 1 6 ) 9 5 9 1 > > > f r o m s h a i m p o r t s h a > > > s h a ( f o o 9 5 9 1 ) . h e x d i g e s t ( ) 0 0 0 0 d e 4 c 9 b 2 7 c e c 9 b 2 0 e 2 0 9 4 7 8 5 c 1 c 5 8 e a f 2 3 9 4 8 > > > s h a ( 1 : 1 6 : 0 4 0 9 2 2 : f o o : : + A r S r t K d : 1 6 4 b 3 ) . h e x d i g e s t ( ) 0 0 0 0 a 9 f e 0 c 6 d b 2 e f c b c a b 1 5 1 5 7 7 3 5 e 7 7 c 0 8 7 7 f 3 4 三 、 应 用 场 景 B i t c o i n 我 们 还 需 要 一 个 类 似 于 A d a m B a c k 提 出 的 h a s h c a s h 。 在 进 行 随 机 散 列 运 算 时 ， 工 作 量 证 明 机 制 引 入 了 对 某 一 个 特 定 值 的 扫 描 工 作 ， 比 方 说 S H A 2 5 6 下 ， 随 机 散 列 值 以 一 个 或 多 个 0 开 始 。 那 么 随 着 0 的 数 目 的 上 升 , 找 到 这 个 解 所 需 要 的 工 作 量 将 呈 指 数 增 长 ， 而 对 结 果 进 行 检 验 则 仅 需 要 一 次 随 机 散 列 运 算 。 我 们 在 区 块 中 补 增 一 个 随 机 数 ， 这 个 随 机 数 要 使 得 该 给 定 区 块 的 随 机 散 列 值 出 现 了 所 需 的 那 么 多 个 0 。 我 们 通 过 反 复 尝 试 来 找 到 这 个 随 机 数 ， 直 到 找 到 为 止 ， 这 样 我 们 就 构 建 了 一 个 工 作 量 证 明 机 制 。 只 要 该 C P U 耗 费 的 工 作 量 能 够 满 足 该 工 作 量 证 明 机 制 ， 那 么 除 非 重 新 完 成 相 当 的 工 作 量 ， 该 区 块 的 信 息 就 不 可 更 改 。 由 于 之 后 的 区 块 是 链 接 在 该 区 块 之 后 的 ， 所 以 想 要 更 改 该 区 块 中 的 信 息 ， 就 还 需 要 重 新 完 成 之 后 所 有 区 块 的 全 部 工 作 量 。 — — 中 本 聪 ( S a t o s h i N a k a m o t o ) 《 比 特 币 : 一 种 点 对 点 的 电 子 现 金 系 统 》 比 特 币 使 用 类 似 h a s h c a s h 算 法 来 作 为 矿 工 的 工 作 量 证 明 ， 在 h a s h c a s h 的 基 础 上 ， 比 特 币 使 用 了 s h a 2 5 6 算 法 ， 在 最 初 的 版 本 中 要 求 3 2 比 特 位 的 前 导 零 ， 然 后 比 特 币 网 络 会 周 期 性 的 重 置 难 度 以 应 对 矿 工 日 益 提 升 的 硬 件 性 能 ， 目 前 的 难 度 级 别 要 求 2 5 6 位 哈 希 7 2 比 特 位 的 前 导 零 。 比 特 币 并 没 有 完 全 照 搬 h a s h c a s h ， 相 对 于 h a s h c a s h ， 比 特 币 做 了 如 下 改 进 ： h a s h c a s h 使 用 了 s h a 1 ( 1 6 0 位 ) ， 而 比 特 币 使 用 了 s h a 2 5 6 ( 2 5 6 位 ) 。 为 了 提 高 安 全 性 ， S a t o s h i 使 h a s h 运 行 了 两 次 。 为 了 确 保 区 块 创 建 率 不 变 （ 1 0 分 钟 出 块 ） ， 周 期 性 调 整 难 度 ( 前 期 3 2 位 零 ， 目 前 7 2 位 零 ) 。 四 、 参 考 链 接 h t t p : / / w w w . h a s h c a s h . o r g h t t p s : / / e n . w i k i p e d i a . o r g / w i k i / H a s h c a s h h t t p : / / w w w . g n o s i s . c x / d o w n l o a d / g n o s i s / u t i l / h a s h c a s h . p y h t t p s : / / w w w . i b m . c o m / d e v e l o p e r w o r k s / c n / l i n u x / l h a s h c a s h . h t m l 版 权 声 明 © 著 作 权 归 作 者 所 有 允 许 自 由 转 载 ， 但 请 保 持 署 名 和 原 文 链 接 。 不 允 许 商 业 用 途 、 盈 利 行 为 及 衍 生 盈 利 行 为 。 图 片 来 源 于 网 络 一 、 基 础 概 念 H a s h c a s h 是 一 个 工 作 量 证 明 （ p r o o f o f w o r k ） 算 法 ， 可 以 用 于 垃 圾 邮 件 过 滤 ， 拒 绝 服 务 攻 击 （ D D O S ） 等 领 域 。 比 特 币 中 挖 矿 算 法 的 工 作 量 证 明 机 制 也 是 基 于 H a s h c a s h 来 实 现 的 。 H a s h c a s h 由 A d a m B a c k 于 1 9 9 7 年 首 次 提 出 ， 论 文 戳 这 里 。 先 来 了 解 一 下 H a s h c a s h 算 法 的 原 理 吧 。 正 如 密 码 学 中 的 . . . Q u e u e : 应 用 于 生 产 者 消 费 者 模 式 的 P y t h o n 队 列 作 者 : 曹 容 端 时 间 : 2 0 1 6 1 0 2 1 分 类 : P y t h o n 7 条 评 论 图 片 来 源 于 网 络 版 权 声 明 © 著 作 权 归 作 者 所 有 允 许 自 由 转 载 ， 但 请 保 持 署 名 和 原 文 链 接 。 不 允 许 商 业 用 途 、 盈 利 行 为 及 衍 生 盈 利 行 为 。 什 么 是 Q u e u e ？ Q u e u e 是 P y t h o n 标 准 库 中 的 线 程 安 全 的 队 列 （ F I F O ） 实 现 ， 提 供 了 一 个 适 用 于 多 线 程 编 程 的 先 进 先 出 的 数 据 结 构 ， 即 队 列 ， 用 来 在 生 产 者 和 消 费 者 （ ） 线 程 之 间 的 信 息 传 递 。 为 什 么 使 用 Q u e u e ， 而 不 是 l i s t 或 者 d i c t ? l i s t 或 者 d i c t 是 非 线 程 安 全 的 ， Q u e u e 是 线 程 安 全 的 也 即 意 味 着 ： 如 果 使 用 l i s t 或 者 d i c t ， 我 们 必 须 把 它 放 到 l o c k 程 序 块 中 （ a c q u i r e 和 r e l e a s e ） ， 以 防 止 发 生 竞 态 条 件 。 使 用 l i s t 或 者 d i c t ， 需 要 考 虑 线 程 同 步 的 问 题 ， 即 需 要 额 外 考 虑 w a i t 和 n o t i f y 。 生 成 者 不 能 向 满 队 列 添 加 数 据 ， 如 果 使 用 l i s t 或 者 d i c t ， 需 要 额 外 的 代 码 实 现 。 Q u e u e 则 封 装 了 C o n d i t i o n 行 为 ， w a i t ( ) n o t i f y ( ) a c q u i r e ( ) r e l e a s e ( ) 满 队 列 问 题 等 等 ， 无 须 额 外 考 虑 。 先 来 了 解 一 些 概 念 生 产 者 消 费 者 模 式 （ P r o d u c e r C o n s u m e r ） P r o d u c e r C o n s u m e r 模 式 是 多 线 程 编 程 中 最 常 用 的 设 计 模 式 。 生 产 者 负 责 生 产 数 据 ， 并 将 数 据 存 入 队 列 ， 消 费 负 责 消 费 数 据 ， 不 断 从 队 列 中 取 数 据 来 使 用 。 这 里 面 有 两 个 条 件 ： 必 须 满 足 线 程 互 斥 条 件 ： 任 何 时 候 最 多 只 允 许 一 个 线 程 访 问 数 据 ， 其 他 线 程 必 须 等 待 。 这 称 为 线 程 互 斥 。 必 须 满 足 线 程 同 步 条 件 ： 线 程 同 步 是 指 线 程 之 间 所 具 有 的 一 种 制 约 关 系 ， 一 个 线 程 的 执 行 依 赖 另 一 个 线 程 的 消 息 ， 当 它 没 有 得 到 另 一 个 线 程 的 消 息 时 应 等 待 ， 直 到 消 息 到 达 时 才 被 唤 醒 。 举 个 例 子 ： 在 线 程 方 式 下 ， 生 产 者 和 消 费 者 各 自 是 一 个 线 程 。 生 产 者 把 数 据 写 入 队 列 ， 消 费 者 从 队 列 读 出 数 据 。 当 队 列 为 空 ， 消 费 者 就 阻 塞 等 待 （ 稍 事 休 息 ） ； 当 队 列 满 （ 达 到 最 大 长 度 ） ， 生 产 者 就 阻 塞 等 待 。 线 程 阻 塞 线 程 阻 塞 通 常 是 指 一 个 线 程 在 执 行 过 程 中 暂 停 ， 以 等 待 某 个 条 件 的 触 发 。 比 如 一 个 线 程 原 子 操 作 下 ， 其 他 的 线 程 都 是 阻 塞 状 态 的 ； 比 如 i n p u t 语 句 等 待 用 户 的 输 入 ， 线 程 也 是 阻 塞 状 态 ； 比 如 当 队 列 任 务 为 空 的 时 候 ， 线 程 等 待 新 的 任 务 ， 这 时 候 线 程 也 是 阻 塞 的 。 线 程 安 全 比 如 一 个 A r r a y L i s t 类 ， 在 添 加 一 个 元 素 的 时 候 ， 它 可 能 会 有 两 步 来 完 成 ： 在 I t e m s [ S i z e ] 的 位 置 存 放 此 元 素 ； 增 大 S i z e 的 值 。 在 单 线 程 运 行 的 情 况 下 ， 如 果 S i z e = 0 ， 添 加 一 个 元 素 后 ， 此 元 素 在 位 置 0 ， 而 且 S i z e = 1 ； 而 如 果 是 在 多 线 程 情 况 下 ， 比 如 有 两 个 线 程 ， 线 程 A 先 将 元 素 1 存 放 在 位 置 0 。 但 是 此 时 C P U 调 度 线 程 A 暂 停 ， 线 程 B 得 到 运 行 的 机 会 。 线 程 B 向 此 A r r a y L i s t 添 加 元 素 2 ， 因 为 此 时 S i z e 仍 然 等 于 0 （ 注 意 ， 我 们 假 设 的 是 添 加 一 个 元 素 是 要 两 个 步 骤 ， 而 线 程 A 仅 仅 完 成 了 步 骤 1 ） ， 所 以 线 程 B 也 将 元 素 存 放 在 位 置 0 。 然 后 线 程 A 和 线 程 B 都 继 续 运 行 ， 都 增 加 S i z e 的 值 ， 结 果 S i z e 等 于 2 。 那 好 ， 我 们 来 看 看 A r r a y L i s t 的 情 况 ， 期 望 的 元 素 应 该 有 2 个 ， 而 实 际 元 素 是 在 0 位 置 ， 造 成 丢 失 元 素 ， 而 且 S i z e 等 于 2 。 这 就 是 “ 线 程 不 安 全 ” 了 。 原 子 操 作 原 子 （ a t o m ） 本 意 是 “ 不 能 被 进 一 步 分 割 的 最 小 粒 子 ” ， 而 原 子 操 作 （ a t o m i c o p e r a t i o n ） 意 为 不 可 被 中 断 的 一 个 或 一 系 列 操 作 。 如 变 量 的 赋 值 ， 不 可 能 一 个 线 程 在 赋 值 ， 到 一 半 切 到 另 外 一 个 线 程 工 作 去 了 ， 这 是 原 子 操 作 。 但 是 一 些 数 据 结 构 的 操 作 ， 比 如 上 述 A r r a y L i s t 的 例 子 ， 添 加 元 素 是 分 成 两 个 步 骤 的 ， 所 以 必 须 要 加 锁 。 加 锁 后 的 操 作 就 可 以 认 为 是 原 子 的 了 。 举 个 小 栗 子 来 加 深 理 解 ： 原 来 在 银 行 办 理 业 务 是 排 队 的 形 式 的 ， 虽 然 也 是 多 线 程 （ 多 个 窗 口 ） ， 但 是 经 常 出 现 有 些 柜 台 人 多 、 有 些 柜 台 人 少 ， 或 者 有 些 柜 台 办 理 完 了 ， 有 些 柜 台 还 排 着 长 队 ， 这 时 候 就 需 要 人 工 来 干 预 ， 很 麻 烦 ， 效 率 不 高 。 现 在 的 银 行 都 是 叫 号 系 统 ， 这 是 一 个 典 型 的 生 产 者 消 费 者 模 式 。 银 行 提 供 四 排 座 椅 （ 队 列 ） ， 每 人 手 上 拿 一 个 号 ， 先 来 先 办 ， 后 来 后 办 （ 先 进 先 出 F i r s t i n F i r s t o u t ） ； 由 叫 号 机 （ 生 产 者 ） 来 打 印 一 个 号 ， 来 一 个 顾 客 打 印 一 个 号 ， 完 了 塞 到 队 尾 ； 当 然 可 以 设 置 一 个 队 列 最 大 数 ， 比 如 1 0 0 人 ， 超 过 1 0 0 人 在 队 列 里 ， 叫 号 机 就 不 打 印 ， 直 到 队 列 有 空 闲 位 置 。 银 行 开 多 个 窗 口 （ 多 个 消 费 者 线 程 ） 从 队 列 里 叫 号 ， 办 完 一 个 ， 再 叫 一 个 。 办 理 的 业 务 是 原 子 性 的 （ 存 或 者 取 都 在 一 个 人 手 上 完 成 ， 中 间 流 程 不 可 分 割 ） 。 也 不 会 同 时 有 多 个 柜 台 操 作 你 的 帐 户 ， 所 以 是 线 程 安 全 的 。 如 果 都 办 理 完 了 ， 叫 号 机 和 柜 台 都 陷 入 了 等 待 状 态 ， 打 一 会 儿 瞌 睡 ， 线 程 阻 塞 ， 直 到 有 新 的 顾 客 来 办 理 业 务 。 三 种 形 式 的 Q u e u e ： F I F O 队 列 图 片 来 源 于 网 络 c l a s s Q u e u e . Q u e u e ( m a x s i z e = 0 ) F I F O 即 F i r s t i n F i r s t O u t , 先 进 先 出 。 Q u e u e 提 供 了 一 个 基 本 的 F I F O 容 器 ， 使 用 方 法 很 简 单 ， m a x s i z e 是 个 整 数 ， 指 明 了 队 列 中 能 存 放 的 数 据 个 数 的 上 限 。 一 旦 达 到 上 限 ， 插 入 会 导 致 阻 塞 ， 直 到 队 列 中 的 数 据 被 消 费 掉 。 如 果 m a x s i z e 小 于 或 者 等 于 0 ， 队 列 大 小 没 有 限 制 。 L I F O 队 列 图 片 来 源 于 网 络 c l a s s Q u e u e . L i f o Q u e u e ( m a x s i z e = 0 ) L I F O 即 L a s t i n F i r s t O u t , 后 进 先 出 。 与 栈 的 类 似 ， 使 用 也 很 简 单 , m a x s i z e 用 法 同 上 P r i o r i t y 队 列 c l a s s Q u e u e . P r i o r i t y Q u e u e ( m a x s i z e = 0 ) 构 造 一 个 优 先 队 列 。 优 先 级 级 别 越 低 的 越 先 出 来 ， m a x s i z e 用 法 同 上 。 常 用 方 法 创 建 一 个 队 列 # m a x s i z e 表 示 队 列 长 度 ， 小 于 1 表 示 队 列 长 度 无 限 。 i m p o r t Q u e u e q = Q u e u e . Q u e u e ( m a x s i z e = 1 0 ) 将 一 个 值 放 入 队 列 # p u t ( i t e m [ , b l o c k [ , t i m e o u t ] ] ) # 参 数 i t e m 为 必 选 参 数 # b l o c k 为 可 选 参 数 ， 默 认 为 T r u e # 如 果 队 列 为 空 且 b l o c k = T r u e ， p u t ( ) 使 得 调 用 线 程 阻 塞 ， 直 到 空 出 一 个 数 据 单 元 。 # 如 果 队 列 为 空 且 b l o c k = F a l s e ， p u t ( ) 将 抛 出 F u l l 异 常 。 # 将 1 0 插 入 队 尾 q . p u t ( 1 0 ) 将 一 个 值 从 队 列 中 取 出 # g e t ( [ b l o c k [ , t i m e o u t ] ] ) # 参 数 b l o c k 为 可 选 参 数 ， 默 认 为 T r u e # 如 果 队 列 为 空 且 b l o c k = T r u e ， g e t ( ) 使 得 调 用 线 程 阻 塞 ， 直 到 有 新 数 据 产 生 。 # 如 果 队 列 为 空 且 b l o c k = F a l s e ， g e t ( ) 将 抛 出 E m p t y 异 常 。 # 从 对 列 头 部 取 出 一 个 数 据 q . g e t ( ) 获 取 队 列 的 大 小 q . q s i z e ( ) 判 断 队 列 是 否 为 空 # 队 列 为 空 返 回 T r u e ， 反 之 返 回 F a l s e q . e m p t y ( ) 判 断 队 列 是 否 已 满 # 队 列 已 满 返 回 T r u e ， 反 之 返 回 F a l s e q . f u l l ( ) t a s k _ d o n e ( ) 意 味 着 之 前 入 队 的 一 个 任 务 已 经 完 成 。 由 队 列 的 消 费 者 线 程 调 用 。 每 一 个 g e t ( ) 调 用 得 到 一 个 任 务 ， 接 下 来 的 t a s k _ d o n e ( ) 调 用 告 诉 队 列 该 任 务 已 经 处 理 完 毕 。 如 果 当 前 一 个 j o i n ( ) 正 在 阻 塞 ， 它 将 在 队 列 中 的 所 有 任 务 都 处 理 完 时 恢 复 执 行 （ 即 每 一 个 由 p u t ( ) 调 用 入 队 的 任 务 都 有 一 个 对 应 的 t a s k _ d o n e ( ) 调 用 ） 。 j o i n ( ) 阻 塞 调 用 线 程 ， 直 到 队 列 中 的 所 有 任 务 被 处 理 掉 。 只 要 有 数 据 被 加 入 队 列 ， 未 完 成 的 任 务 数 就 会 增 加 。 当 消 费 者 线 程 调 用 t a s k _ d o n e ( ) （ 意 味 着 有 消 费 者 取 得 任 务 并 完 成 任 务 ） ， 未 完 成 的 任 务 数 就 会 减 少 。 当 未 完 成 的 任 务 数 降 到 0 ， j o i n ( ) 解 除 阻 塞 。 其 他 q . p u t _ n o w a i t ( i t e m ) = = q . p u t ( i t e m , F a l s e ) q . g e t _ n o w a i t ( ) = = q . g e t ( F a l s e ) 一 个 最 简 单 的 生 产 者 消 费 者 模 式 # c o d i n g : u t f 8 # f i l e n a m e : q u e u e . p y # a u t h o r : c a o r d @ s h o w w a n t . c o m i m p o r t t i m e i m p o r t Q u e u e i m p o r t t h r e a d i n g c l a s s P r o d u c e r ( t h r e a d i n g . T h r e a d ) : d e f _ _ i n i t _ _ ( s e l f , t h r e a d _ n a m e , q u e u e ) : t h r e a d i n g . T h r e a d . _ _ i n i t _ _ ( s e l f , n a m e = t h r e a d _ n a m e ) s e l f . d a t a = q u e u e d e f r u n ( s e l f ) : f o r i i n r a n g e ( 2 0 ) : p r i n t ( % s : % s i s p r o d u c i n g % d t o t h e q u e u e ! % ( t i m e . c t i m e ( ) , s e l f . g e t N a m e ( ) , i ) ) s e l f . d a t a . p u t ( i ) t i m e . s l e e p ( 1 ) p r i n t ( % s : % s f i n i s h e d ! % ( t i m e . c t i m e ( ) , s e l f . g e t N a m e ( ) ) ) t i m e . s l e e p ( 1 0 ) f o r i i n r a n g e ( 1 0 ) : s e l f . d a t a . p u t ( i ) c l a s s C o n s u m e r ( t h r e a d i n g . T h r e a d ) : d e f _ _ i n i t _ _ ( s e l f , t h r e a d _ n a m e , q u e u e ) : t h r e a d i n g . T h r e a d . _ _ i n i t _ _ ( s e l f , n a m e = t h r e a d _ n a m e ) s e l f . d a t a = q u e u e d e f r u n ( s e l f ) : w h i l e 1 : t r y : n u m = s e l f . d a t a . g e t ( ) p r i n t ( % s : % s i s c o n s u m i n g . % d i n t h e q u e u e i s c o n s u m e d ! % ( t i m e . c t i m e ( ) , s e l f . g e t N a m e ( ) , n u m ) ) e x c e p t : p r i n t ( % s : % s f i n i s h e d ! % ( t i m e . c t i m e ( ) , s e l f . g e t N a m e ( ) ) ) # b r e a k d e f m a i n ( ) : q u e u e = Q u e u e . Q u e u e ( m a x s i z e = 2 0 ) p r o d u c e r = P r o d u c e r ( p r o d u c e r , q u e u e ) c o n s u m e r = C o n s u m e r ( c o n s u m e r , q u e u e ) p r o d u c e r . s t a r t ( ) c o n s u m e r . s t a r t ( ) p r o d u c e r . j o i n ( ) c o n s u m e r . j o i n ( ) p r i n t ( A l l t h r e a d f i n i s h e d ) i f _ _ n a m e _ _ = = _ _ m a i n _ _ : m a i n ( ) 图 片 来 源 于 网 络 版 权 声 明 © 著 作 权 归 作 者 所 有 允 许 自 由 转 载 ， 但 请 保 持 署 名 和 原 文 链 接 。 不 允 许 商 业 用 途 、 盈 利 行 为 及 衍 生 盈 利 行 为 。 什 么 是 Q u e u e ？ Q u e u e 是 P y t h o n 标 准 库 中 的 线 程 安 全 的 队 列 （ F I F O ） 实 现 ， 提 供 了 一 个 适 用 于 多 线 程 编 程 的 先 进 先 出 的 数 据 结 构 ， 即 队 列 ， 用 来 在 生 产 者 和 消 费 者 （ ） 线 程 之 间 的 信 息 传 递 。 为 什 么 使 用 Q u e u . . . 深 入 浅 出 P y t h o n 多 线 程 （ 1 ） 创 建 线 程 作 者 : 曹 容 端 时 间 : 2 0 1 6 1 0 0 5 分 类 : P y t h o n 1 条 评 论 图 片 来 源 于 网 络 T h r e a d 对 象 T h r e a d 对 象 位 于 P y t h o n 标 准 库 中 的 t h r e a d i n g . p y 中 。 它 的 初 始 化 方 法 是 这 样 的 ： d e f _ _ i n i t _ _ ( s e l f , g r o u p = N o n e , t a r g e t = N o n e , n a m e = N o n e , a r g s = ( ) , k w a r g s = N o n e , * , d a e m o n = N o n e ) 一 个 线 程 通 过 调 用 其 s t a r t ( ) 方 法 来 激 活 ， 每 个 线 程 对 象 只 能 调 用 一 次 s t a r t ( ) ， 否 则 会 抛 出 R u n t i m e E r r o r 错 误 。 假 设 我 们 现 在 有 一 场 跑 步 比 赛 ， 共 有 5 名 运 动 员 参 加 。 发 令 枪 一 响 ， 大 家 肯 定 同 时 开 始 跑 （ 并 发 ） ， 直 到 所 有 的 运 动 员 跑 完 ， 比 赛 结 束 。 在 这 个 例 子 里 面 ， 我 们 可 以 把 赛 场 看 成 是 一 个 进 程 ， 而 赛 场 里 面 的 每 个 运 动 员 占 用 一 条 跑 道 ， 这 个 是 线 程 。 发 令 枪 一 响 ， 所 有 线 程 启 动 ， 直 到 运 行 结 束 。 让 我 们 模 拟 一 下 上 述 场 景 ， 我 们 可 以 用 两 种 方 式 来 实 现 。 为 了 模 拟 跑 步 ， 我 们 引 入 一 个 r a n d o m 来 产 生 一 个 随 机 事 件 ， 然 后 使 用 t i m e . s l e e p 模 拟 跑 步 用 时 ， 尽 量 使 得 结 果 看 起 来 像 那 么 回 事 : ) 使 用 函 数 创 建 线 程 i m p o r t t i m e i m p o r t r a n d o m i m p o r t t h r e a d i n g d e f r u n n e r ( n a m e ) : t i m e _ c o s t = r a n d o m . r a n d i n t ( 7 , 1 2 ) p r i n t ( : 我 开 始 跑 了 . f o r m a t ( n a m e ) ) t i m e . s l e e p ( t i m e _ c o s t ) p r i n t ( : 我 跑 完 了 ， 用 时 秒 . f o r m a t ( n a m e , t i m e _ c o s t ) ) i f _ _ n a m e _ _ = = _ _ m a i n _ _ : # 我 们 有 5 个 运 动 员 ， 创 建 5 个 线 程 ， 分 别 调 用 s t a r t 方 法 激 活 线 程 n a m e _ l i s t = [ 张 三 , 李 四 , 王 五 , 赵 六 , 何 二 ] f o r n a m e i n n a m e _ l i s t : t = t h r e a d i n g . T h r e a d ( t a r g e t = r u n n e r , a r g s = ( n a m e , ) ) t . s t a r t ( ) 在 这 个 例 子 中 ： 我 们 定 义 了 一 个 r u n n e r 函 数 ， 来 模 拟 跑 步 的 行 为 。 我 们 通 过 实 例 化 t h r e a d i n g . T h r e a d 类 来 创 建 线 程 。 在 这 个 例 子 中 ， 由 于 r u n n e r 函 数 是 一 个 带 参 数 的 函 数 ， 我 们 还 通 过 a r g s 把 参 数 传 给 了 r u n n e r 最 后 分 别 调 用 线 程 对 象 的 s t a r t 方 法 ， 来 开 启 线 程 。 # 运 行 结 果 张 三 : 我 开 始 跑 了 李 四 : 我 开 始 跑 了 王 五 : 我 开 始 跑 了 赵 六 : 我 开 始 跑 了 何 二 : 我 开 始 跑 了 李 四 : 我 跑 完 了 ， 用 时 7 秒 赵 六 : 我 跑 完 了 ， 用 时 8 秒 何 二 : 我 跑 完 了 ， 用 时 8 秒 张 三 : 我 跑 完 了 ， 用 时 1 1 秒 王 五 : 我 跑 完 了 ， 用 时 1 1 秒 我 们 发 现 ， 几 乎 第 一 时 间 ， 5 个 人 都 打 印 了 我 开 始 跑 了 ， 最 后 ， 李 四 得 了 第 一 名 。 通 过 继 承 T h r e a d 类 来 创 建 线 程 当 然 ， 我 们 也 可 以 编 写 面 向 对 象 的 代 码 ， 通 过 继 承 T h r e a d 类 来 实 现 上 面 的 功 能 。 i m p o r t t i m e i m p o r t r a n d o m i m p o r t t h r e a d i n g c l a s s R u n n e r ( t h r e a d i n g . T h r e a d ) : d e f _ _ i n i t _ _ ( s e l f , n a m e ) : s u p e r ( ) . _ _ i n i t _ _ ( n a m e = n a m e ) d e f r u n ( s e l f ) : t i m e _ c o s t = r a n d o m . r a n d i n t ( 7 , 1 2 ) p r i n t ( : 我 开 始 跑 了 . f o r m a t ( s e l f . n a m e ) ) t i m e . s l e e p ( t i m e _ c o s t ) p r i n t ( : 我 跑 完 了 ， 用 时 秒 . f o r m a t ( s e l f . n a m e , t i m e _ c o s t ) ) i f _ _ n a m e _ _ = = _ _ m a i n _ _ : # 我 们 有 5 个 运 动 员 ， 实 例 化 5 个 R u n n e r 对 象 ， 分 别 调 用 s t a r t 方 法 激 活 线 程 n a m e _ l i s t = [ 张 三 , 李 四 , 王 五 , 赵 六 , 何 二 ] f o r n a m e i n n a m e _ l i s t : t = R u n n e r ( n a m e ) t . s t a r t ( ) 在 这 个 例 子 中 ： 我 们 创 建 了 一 个 类 R u n n e r ， 让 它 继 承 自 t h r e a d i n g . T h r e a d 。 在 构 造 器 中 我 们 使 用 s u p e r ( ) 来 调 用 父 类 的 构 造 器 ， 并 且 把 n a m e 传 给 他 。 继 承 T h r e a d 来 实 现 多 线 程 最 重 要 的 是 o v e r r i d e 父 类 的 r u n 方 法 ， 我 们 把 跑 步 的 逻 辑 放 在 r u n 方 法 里 面 。 最 后 跟 上 个 例 子 的 逻 辑 类 似 ， 只 是 我 们 通 过 实 例 化 R u n n e r 类 来 创 建 了 线 程 。 以 上 就 是 P y t h o n 创 建 线 程 的 两 种 方 式 。 两 种 方 式 如 何 选 择 继 承 T h r e a d 类 的 方 式 虽 然 可 行 ， 但 是 这 样 的 实 现 方 式 是 依 赖 t h r e a d i n g 库 的 ， 代 码 只 能 在 线 程 上 下 文 中 使 用 。 而 第 一 种 方 式 ， 实 现 的 代 码 可 以 脱 离 线 程 上 下 文 ， 可 以 在 其 他 上 下 文 使 用 。 如 果 业 务 逻 辑 简 单 ， 推 荐 第 一 种 方 式 （ 使 用 函 数 创 建 线 程 ） 。 如 果 业 务 相 对 复 杂 ， 但 只 跟 线 程 相 关 ， 推 荐 第 二 种 方 式 （ 通 过 继 承 T h r e a d 类 来 创 建 线 程 ） 。 如 果 逻 辑 相 对 复 杂 ， 又 不 是 纯 线 程 业 务 的 ， 可 以 实 现 一 个 类 ， 还 是 以 实 例 化 T h r e a d 类 ， t a r g e t 传 参 数 的 方 式 去 做 ， 比 如 ： c l a s s R u n n e r ( o b j e c t ) : d e f _ _ i n i t _ _ ( s e l f , n a m e ) : s e l f . n a m e = n a m e d e f s t a r t ( s e l f ) : t = t h r e a d i n g . T h r e a d ( t a r g e t = s e l f . r u n ) t . s t a r t ( ) d e f r u n ( s e l f ) : # 线 程 逻 辑 p a s s . . . 节 外 生 枝 在 我 们 上 面 的 例 子 中 ， 我 们 很 好 的 实 现 了 模 拟 赛 跑 的 一 个 效 果 。 但 是 别 高 兴 的 太 早 ， 这 时 候 主 办 方 ( 产 品 经 理 ) 找 过 来 了 ， 说 你 程 序 是 跑 完 了 ， 但 是 还 没 有 宣 布 比 赛 结 束 ， 最 后 你 得 打 印 出 一 行 比 赛 结 束 才 行 。 这 还 不 简 单 ， 不 就 是 最 后 加 一 个 打 印 吗 ？ . . . i f _ _ n a m e _ _ = = _ _ m a i n _ _ : # 我 们 有 5 个 运 动 员 ， 实 例 化 5 个 R u n n e r 对 象 ， 分 别 调 用 s t a r t 方 法 激 活 线 程 n a m e _ l i s t = [ 张 三 , 李 四 , 王 五 , 赵 六 , 何 二 ] f o r n a m e i n n a m e _ l i s t : t = R u n n e r ( n a m e ) t . s t a r t ( ) p r i n t ( 比 赛 结 束 ) 我 们 来 看 看 结 果 ： 张 三 : 我 开 始 跑 了 李 四 : 我 开 始 跑 了 王 五 : 我 开 始 跑 了 赵 六 : 我 开 始 跑 了 何 二 : 我 开 始 跑 了 比 赛 结 束 王 五 : 我 跑 完 了 ， 用 时 8 秒 张 三 : 我 跑 完 了 ， 用 时 9 秒 李 四 : 我 跑 完 了 ， 用 时 9 秒 何 二 : 我 跑 完 了 ， 用 时 9 秒 赵 六 : 我 跑 完 了 ， 用 时 1 2 秒 W T F ， 大 写 的 黑 人 问 号 ， 还 没 跑 完 就 打 印 啦 ， 这 不 科 学 啊 。 下 一 小 节 ， 让 我 们 来 试 着 分 析 并 解 决 这 个 不 同 寻 常 的 问 题 吧 。 版 权 声 明 © 著 作 权 归 作 者 所 有 允 许 自 由 转 载 ， 但 请 保 持 署 名 和 原 文 链 接 。 不 允 许 商 业 用 途 、 盈 利 行 为 及 衍 生 盈 利 行 为 。 图 片 来 源 于 网 络 T h r e a d 对 象 T h r e a d 对 象 位 于 P y t h o n 标 准 库 中 的 t h r e a d i n g . p y 中 。 它 的 初 始 化 方 法 是 这 样 的 ： d e f _ _ i n i t _ _ ( s e l f , g r o u p = N o n e , t a r g e t = N o n e , n a m e = N o n e , a r g s = ( ) , k w a r g s = N o n e , * , d a e m o n = N o n e ) 一 个 线 程 通 过 调 用 . . . 1 2 3 后 一 页 » 分 类 P y t h o n ( 1 0 ) G o l a n g ( 0 ) B l o c k c h a i n ( 0 ) A l g o r i t h m ( 1 ) 最 新 文 章 配 置 文 件 用 H O C O N / . c o n f 还 是 j s o n P y t h o n R e c o r d s 库 使 用 详 解 工 作 量 证 明 之 H a s h c a s h 算 法 ， 了 解 一 下 ？ Q u e u e : 应 用 于 生 产 者 消 费 者 模 式 的 P y t h o n 队 列 深 入 浅 出 P y t h o n 多 线 程 （ 1 ） 创 建 线 程 深 入 浅 出 P y t h o n 多 线 程 （ 0 ） G I L 全 局 解 释 器 锁 的 前 世 今 生 P y t h o n 使 用 S A X 处 理 x m l 文 件 P y t h o n 抓 取 同 花 顺 股 市 直 播 P y t h o n 开 发 的 一 些 技 巧 P y t h o n 对 象 的 赋 值 、 浅 拷 贝 和 深 拷 贝 机 制 最 近 回 复 w a h p : o r a c l e 连 不 上 热 搜 榜 : 文 章 还 不 错 ， 支 持 一 下 今 日 新 鲜 事 : 文 章 非 常 好 超 喜 欢 今 日 新 闻 : 文 章 不 错 支 持 一 下 吧 头 条 新 闻 : 文 章 不 错 非 常 喜 欢 今 日 新 鲜 事 : 文 章 不 错 支 持 一 下 吧 热 搜 榜 : 文 章 不 错 非 常 喜 欢 头 条 : 文 章 不 错 支 持 一 下 吧 热 搜 : 文 章 不 错 非 常 喜 欢 今 日 新 闻 : 文 章 不 错 非 常 喜 欢 其 它 登 录 文 章 R S S 评 论 R S S T y p e c h o © 2 0 2 4 人 生 苦 短 . 由 T y p e c h o 强 力 驱 动 . 苏 I C P 备 1 6 0 6 4 0 7 0 号

站点概括

关于www.caorongduan.com说明：
www.caorongduan.com由网友主动性提交被聚集网整理收录的，聚集网仅提供www.caorongduan.com的基础信息并免费向大众网友展示，www.caorongduan.com的是IP地址：114.215.114.30 [中国山东青岛 阿里云]，www.caorongduan.com的百度权重为0、百度手机权重为0、百度收录为0条、360收录为0条、搜狗收录为0条、谷歌收录为0条、百度来访流量大约在-之间、百度手机端来访流量大约在-之间、www.caorongduan.com的备案号是登录可见、备案人叫登录可见、被百度收录的关键词有0个、手机端关键词有0个、该站点迄今为止已经创建9年7个月5天。

内容声明：

1、本站收录的内容来源于大数据收集，版权归原网站所有！
2、本站收录的内容若侵害到您的利益，请联系我们进行删除处理！
3、本站不接受违规信息，如您发现违规内容，请联系我们进行清除处理！
4、本文地址：http://www.jujiwang.com/links/6e87404eedb3198cea87.html，复制请保留版权链接！

---