(换肤)
语言：
Γ(z)Γ(1-z) = π/sin(πz)(Γ(z)Γ(1-z))
Γ函数，又称伽马函数，是一个推广阶乘函数到复平面的函数，它的定义如下，Γ，z，=∫0tz，1e，tdt对于正整数n，Γ，n，=，n，1，Γ函数满足以下乘积公式，Γ，z，Γ，1，z，=π，sin，πz，这个公式可以用来求解许多积分，例如，∫0tα，1，1，t，β，1dt=B，α，β，Γ，α，Γ，β，其中B，α，β，是贝塔函数，证明我...。
技术教程 2024-09-12 13:42:55
Γ(n) = (n-1)!(Γn+1)
Γ，伽马，函数是一种推广阶乘的概念，表示实数和复数的函数，它与阶乘函数有密切的关系，可以通过将阶乘函数连续化来获得Γ函数，有关Γ函数的展开内容，请参阅维基百科的条目，Γ函数的递推公式Γ函数具有以下递推公式，Γ，n，=，n，1，其中，n是一个正整数，n，1，是，n，1，的阶乘这个递推公式表明，一个正整数的Γ函数值等于其前一个整数的阶...。
互联网资讯 2024-09-12 13:35:09
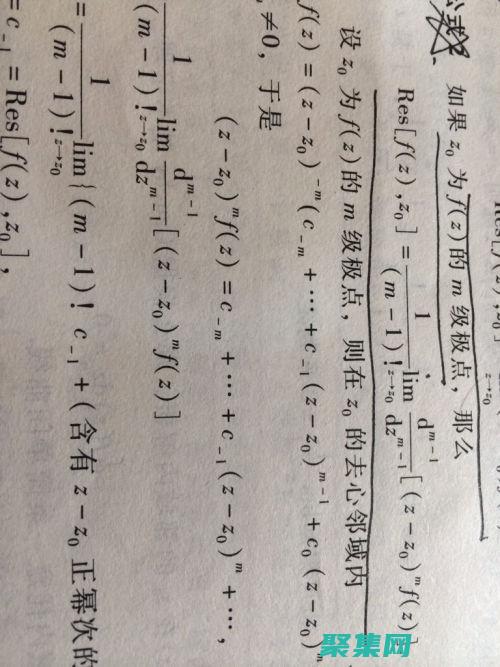Γ(z+1) = zΓ(z)
Γ函数是一个在复平面上的特殊函数，在数学和物理中有着广泛的应用，它具有以下递推关系，Γ，z，1，=zΓ，z，这个关系可以通过积分表示来证明，Γ，z，1，=∫0tze，tdt并使用积分byparts，Γ，z，1，=，tze，t，0，z∫0tz，1e，tdt显然，第一个项为0，因此，Γ，z，1，=z∫0tz，1e，tdt将t=u带入积分，...。
最新资讯 2024-09-12 13:32:09
gamma 函数表：一个全面的工具，用于理解和应用 gamma 函数的数学属性(gamma函数)
伽马函数是数学中一个重要的特殊函数，在概率论、统计学和应用数学中有着广泛的应用，该函数可以表示为，Γ，z，=∫0tz，1e，tdt其中z是一个复数，伽马函数具有许多有用的性质，包括，Γ，z，1，=zΓ，z，Γ，n，=，n，1，Γ，1，2，=√πΓ，z，Γ，1，z，=π，sin，πz，伽马函数表是一个有价值的工具，用于理解和应用伽马函...。
本站公告 2024-09-12 13:29:49
gamma 函数表：探索其在积分、概率和特殊函数中的用法(gamma函数公式)
Γ函数，伽马函数，是一个广义的阶乘函数，具有以下性质，$$\Gamma，z，1，=z\Gamma，z，\quadz\in\mathbb，C，$$Γ函数在许多领域都有广泛的应用，包括积分、概率和特殊函数，下表总结了Γ函数的一些重要公式和用法，公式用法$$\Gamma，z，=\int，0^\inftyt^，z，1，e^，t，dt，\q...。
互联网资讯 2024-09-12 13:06:07
γ 分布密度函数的未来：统计学和概率论中的不断发展 (分布密度函数简写)
γ分布密度函数，又称伽马分布密度函数，在统计学和概率论中有着广泛的应用，它是一种非负连续分布，具有灵活性高的形状和尺度参数，使其能够对各种类型的随机变量进行建模，γ分布的应用γ分布密度函数在以下领域有着广泛的应用，寿命分析，伽马分布常用于建模材料、设备和组件的寿命数据，金融，伽马分布用于建模金融数据的分布，例如股票收益率和资产价值，保...。
互联网资讯 2024-09-09 08:43:23
揭秘 γ 分布密度函数的性质：从形状到中心趋势 (分布密度概念)
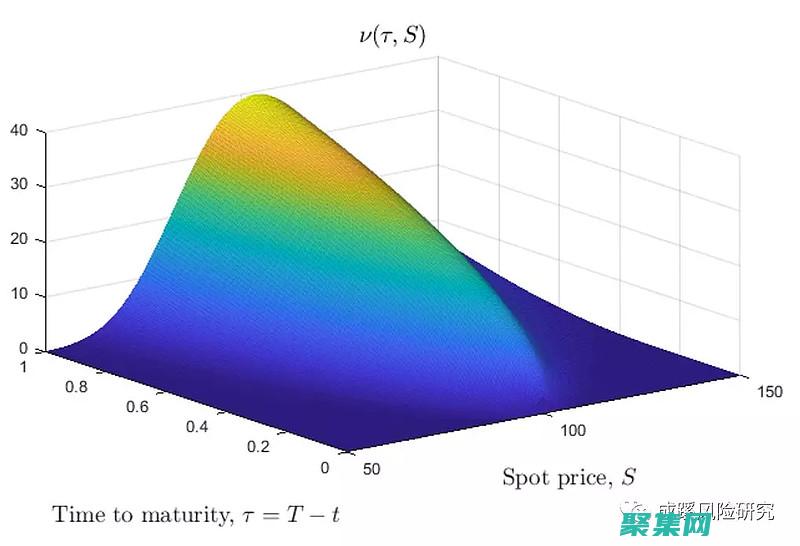
θ的形状参数γ分布密度函数的形状由其形状参数θ控制，θ越大，分布的峰值越高，分布越集中，相反，θ越小，分布的峰值越低，分布越分散，θ的值还决定了分布的偏态性，当θ<，1时，分布向左偏，当θ>，1时，分布向右偏，r的速率参数γ分布密度函数的速率参数r控制着分布的中心趋势，r越大，分布的中心越靠左，分布越偏向于较小的值，相反，r越...。
技术教程 2024-09-09 08:39:18
γ 分布密度函数的数学基础：从基本原理到高级定理 (分布密度函数简写)
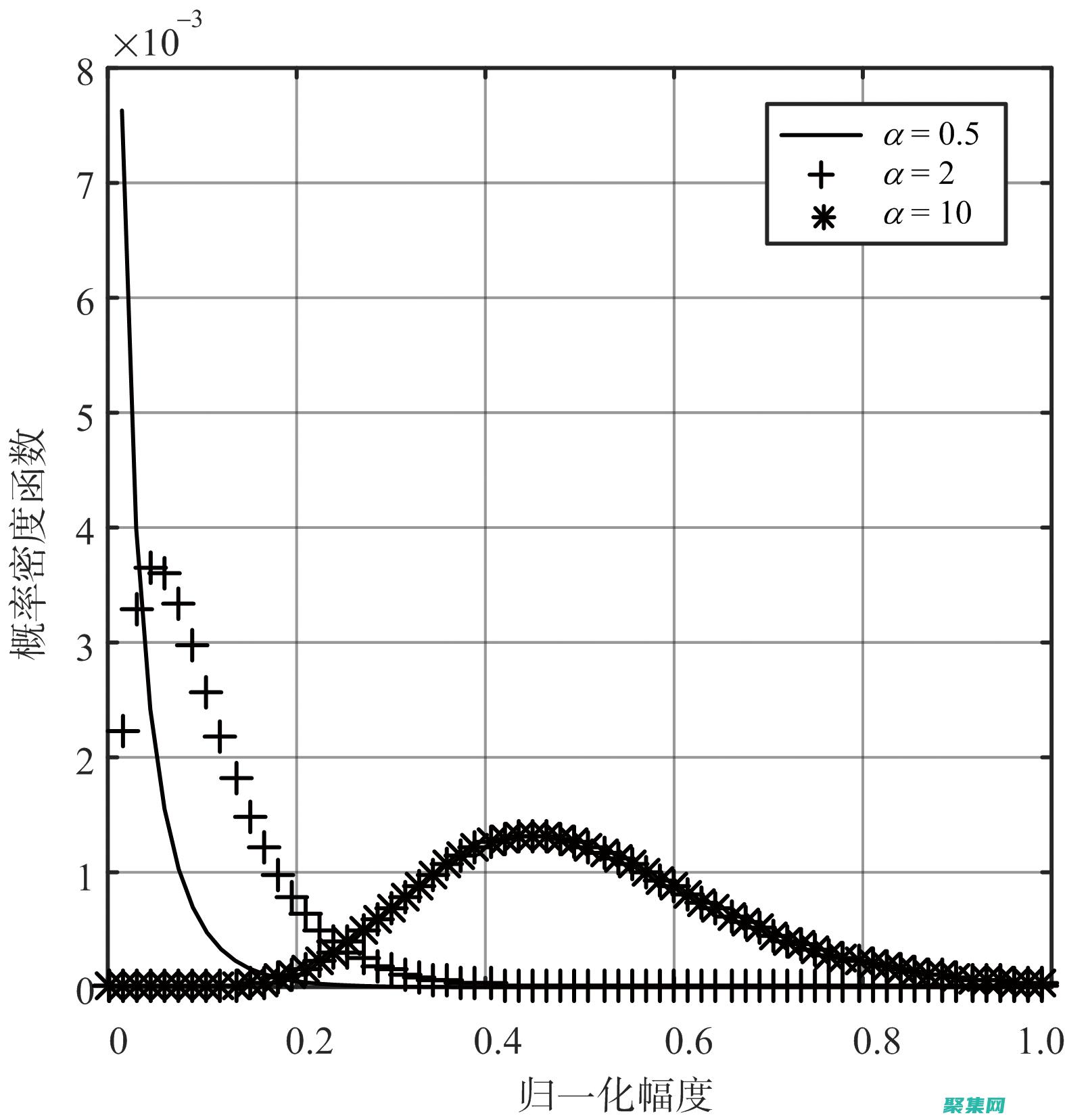
基本原理γ分布是一种连续概率分布，用于描述具有正实随机变量的各种现象，其概率密度函数，PDF，为，$$f，x，\alpha，\beta，=\frac，\beta^\alpha，\Gamma，\alpha，x^，\alpha，1，e^，\betax，$$其中，$x$是随机变量$\alpha$是形状参数$\beta$是速率参数$\G...。
本站公告 2024-09-09 08:38:06
探索 γ 分布密度函数的应用领域：从金融到工程 (分布密集)
引言Γ分布是一种连续概率分布，它以其广泛的形状和规模参数而闻名，使其具有高度的灵活性，由于其多功能性，Γ分布在金融、工程和统计等众多领域中有着广泛的应用，Γ分布密度函数Γ分布的概率密度函数为，f，x，=，λ^α，Γ，α，x^，α，1，e^，λx，其中，α是形状参数λ是尺度参数Γ，α，是Γ函数，定义为，Γ，α，=∫0^∞t^，α，1...。
最新资讯 2024-09-09 08:36:31
γ 分布密度函数的魔力：理解其在统计模型中的作用 (分布密度函数简写)
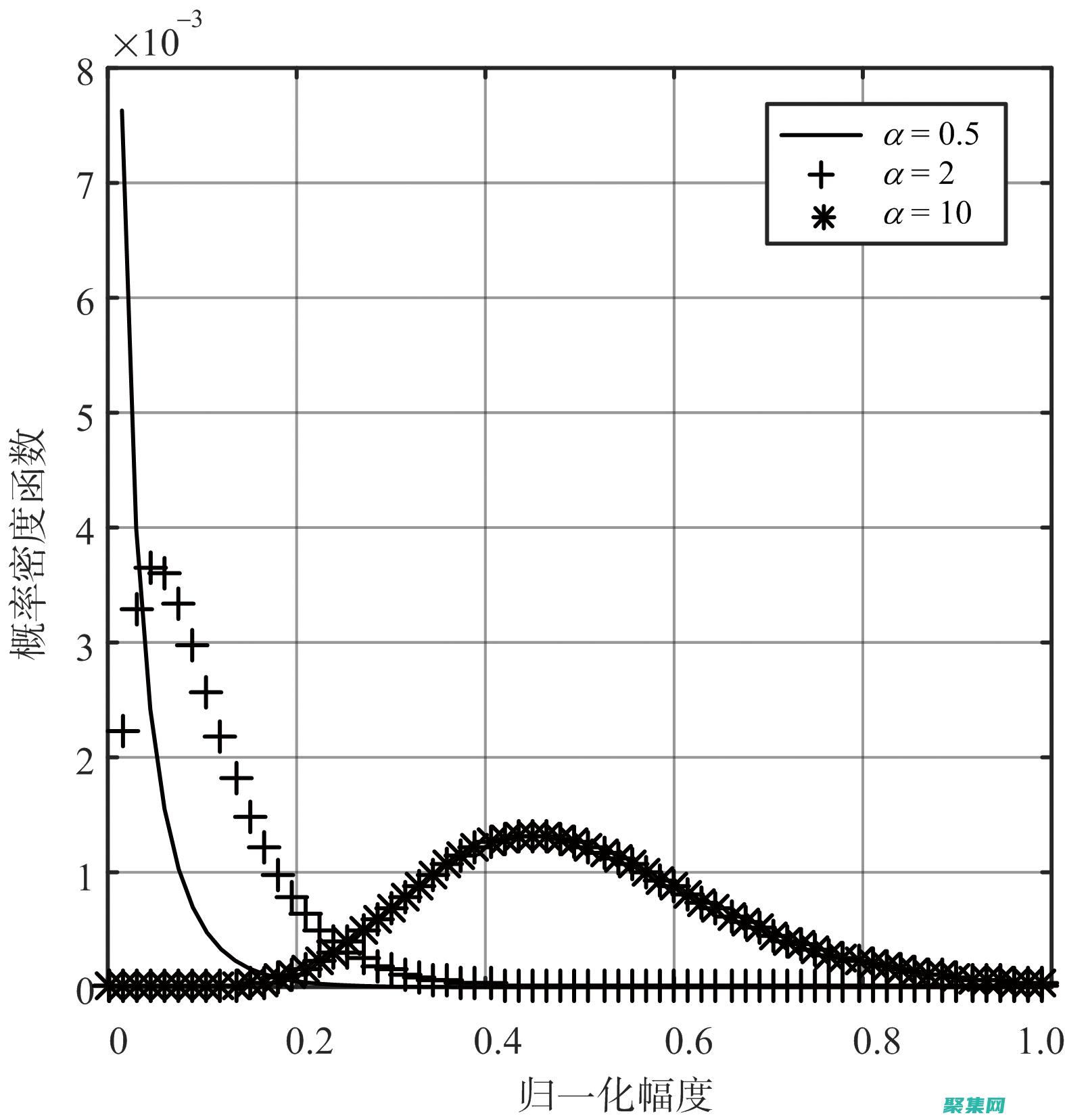
简介γ分布，也称为伽马分布，是一种连续概率分布，广泛应用于统计建模中，其密度函数具有独特的形状，使其特别适合对正偏数据进行建模，在本文中，我们将深入了解γ分布密度函数，并探索它在统计模型中的广泛应用，γ分布密度函数γ分布密度函数由以下公式给出，```f，x，α，β，=，β^α，Γ，α，x^，α，1，exp，βx，```其中，x是随...。
技术教程 2024-09-09 08:35:26
揭开γ 分布密度函数的神秘面纱：统计学中的基本构建块 (分布密度概念)
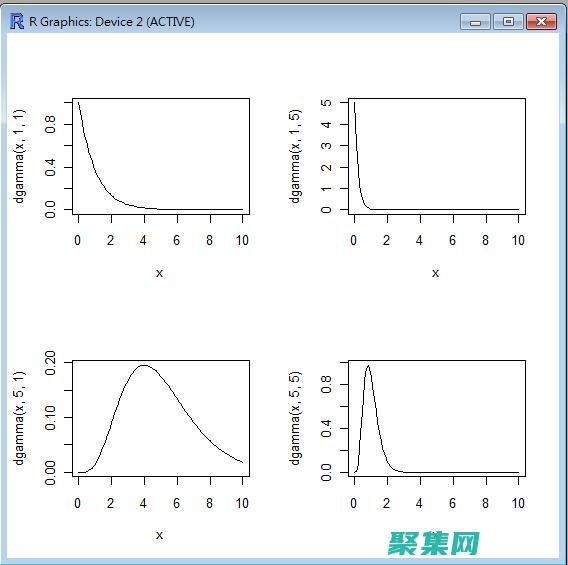
引言在统计学领域，概率分布在描述随机变量的行为方面发挥着至关重要的作用，这些分布提供了对数据分布和可变性的见解，从而使我们能够进行预测、做出决策并检验假设，在所有概率分布中，γ分布是一个特别重要的分布，在各种应用中发挥着关键作用，什么是γ分布，γ分布，也称为伽马分布，是一种连续概率分布，它描述了非负随机变量的行为，它有两种形状参数，α...。
最新资讯 2024-09-09 08:32:49
γ 分布密度函数的解读：从零到无限的探索之旅 (β分布密度函数)
简介γ分布，又称伽马分布，是一种连续概率分布，广泛应用于概率论和统计学中，其概率密度函数被定义为，f，x，=，x^α，1，e^，x，β，Γ，α，β^α，其中，α和β分别为形状参数和尺度参数，Γ，·，为伽马函数，函数图像γ分布密度的形状取決于其形状参数α，α<，1，曲线向右偏，具有右尾比左尾更长的分布，α=1，曲线呈指数分布，...。
互联网资讯 2024-09-09 08:31:37
了解 γ 分布的数学奥秘：深入探讨其密度函数 (x²分布的定义)
概述γ分布，伽马分布，，又称x²，卡方，分布，是一个连续概率分布，常用于建模非负随机变量，它具有广泛的应用，包括统计推断、贝叶斯分析和风险评估，密度函数γ分布的密度函数定义为，```f，x，α，β，=，β^αx^，α，1，e^，βx，Γ，α，```其中，x是非负随机变量α是形状参数，控制分布的形状β是速率参数，控制分布的尺度Γ，...。
本站公告 2024-09-09 08:29:51
Gamma 函数的计算技巧：从近似值到高效算法 (gamma函数)
引言伽马函数在数学、统计学和物理学中有着广泛的应用，它的计算通常是困难和耗时的，本文将介绍一系列技巧，用于估算和精确计算伽马函数，近似值对于较大的自变量，伽马函数可以用斯特林近似公式近似，Γ，z，≈√，2πz，z，e，z高效算法算法1，收敛级数对于，z，<，1，伽马函数可以用收敛级数表示，Γ，z，=Γ，z，1，z算法2，递推公...。
互联网资讯 2024-09-08 12:26:55
Gamma 函数与数论之间的深刻联系：一个数学之旅 (gamma函数公式)
前言Γ函数，以数学家莱昂哈德·欧拉的名字命名，是一个以其广泛的应用而闻名的特殊函数，它在数论中有着深刻的联系，为理解许多数论问题提供了关键的见解，Γ函数Γ函数定义为对于所有复数z，除了z=0，1，2，...，，其中Re，z，>，0，Γ，z，=∫0tz，1e，tdt它具有以下重要的性质，Γ，z，1，=zΓ，z，Γ，1，=1Γ，n...。
技术教程 2024-09-08 12:25:56
Gamma 函数的分布和统计应用：从随机变量到概率分布 (gamma函数)
简介Gamma函数是一个广义的阶乘函数，它将正实数映射到正实数，它在概率论和统计学中有着广泛的应用，特别是在连续概率分布和随机变量的建模中，Gamma分布Gamma分布是一个连续概率分布，其概率密度函数为，αxα，1e，αx，Γ，α，其中α是形状参数，x是随机变量，Gamma分布具有高度的可塑性，它可以模拟各种不同的形状，从指数衰减到...。
最新资讯 2024-09-08 12:23:38
利用 Gamma 函数解决复杂积分：一步一步的指南 (利用gamma制作一个有趣的ppt)
Gamma函数是一个重要的特殊函数，在数学和物理的各个领域都有应用，它可以用来解决广泛的积分，包括复杂的积分，在本文中，我们将一步一步地介绍如何使用Gamma函数来解决复杂积分，第一步，理解Gamma函数Gamma函数Γ，z，定义为$$\Gamma，z，=\int，0^\inftyt^，z，1，e^，t，dt$$其中z是一个复数，G...。
本站公告 2024-09-08 12:22:13
Gamma 函数与特殊函数之间的联系：一个深入的探索 (gamma函数)
Gamma函数在数学领域中有着广泛的应用，它与许多特殊函数有着密切的联系，本文将深入探讨Gamma函数与这些特殊函数之间的关系，揭示其内在的关联性，伽马函数的定义伽马函数是一个解析函数，用于扩展阶乘函数到复数域，它定义为以下积分，Γ，z，=∫0tz，1e，tdt其中z是复数，Gamma函数与阶乘函数Gamma函数与阶乘函数密切相关，当...。
技术教程 2024-09-08 12:21:06
揭开 Gamma 函数的神秘面纱：从定义到性质 (揭开膏药可以直接洗澡吗)
Gamma函数，记作Γ，z，，是数学中一个重要的特殊函数，具有深远的理论和应用意义，它可以被看作阶乘函数在复数域上的推广，在概率、统计、物理和工程等领域有着广泛的应用，1.定义Gamma函数的定义如下，其中，z是一个复数，且Re，z，>，0，2.性质Gamma函数具有许多重要的性质，包括，自变量关系，Γ，z，1，=zΓ，z，因子分...。
本站公告 2024-09-08 12:15:39
Gamma 函数：深入探索其数学和应用 (gamma函数公式)
引言Gamma函数是一个在数学和应用科学中至关重要的特殊函数，它广泛应用于概率统计、金融、物理学和工程学等领域，本文将深入探讨Gamma函数的数学性质、公式和应用，帮助读者全面理解这一重要的函数，Gamma函数的数学定义Gamma函数Γ，z，被定义为以下积分，Γ，z，=∫0tz，1e，tdt其中z是一个复数，Re，z，>，0，Ga...。
本站公告 2024-09-08 12:14:21
计算不完全 Gamma 函数的各种方法：数值技巧和理论分析 (计算不完全,是否重算后再保存)
简介不完全Gamma函数是一个广泛应用于各种科学和工程领域的数学函数，它有两种主要类型，上不完全Gamma函数和下不完全Gamma函数，上不完全Gamma函数表示为，```Γ，α，x，=∫0xtα，1e，tdt```而下不完全Gamma函数表示为，```γ，α，x，=∫xtα，1e，tdt=Γ，α，Γ，α，x，```其中，α是一个复...。
技术教程 2024-09-07 13:41:14
不完全 Gamma 函数的应用：发现其在概率和统计中的重要性 (不完全gamma 函数)
引言不完全Gamma函数是一个在概率和统计中具有广泛应用的特殊函数，它通过将Gamma函数与积分相结合来定义，提供了分析分布和概率的强大工具，不完全Gamma函数的定义不完全Gamma函数γ，s，x，定义为，γ，s，x，=∫0xts，1e，tdt其中s是一个复参数，x是一个实参数，不完全Gamma函数的性质不完全Gamma函数具有以下...。
技术教程 2024-09-07 13:38:45
了解不完全 Gamma 函数的奥秘：定义、公式和性质 (不完全解理)
前言Gamma函数在概率论、统计学和应用数学等领域有着广泛的应用，为了扩展Gamma函数的适用范围，数学家们提出了不完全Gamma函数的概念，文章将带你深入理解不完全Gamma函数的定义、公式和性质，揭开它神秘的面纱，定义不完全Gamma函数，记为Γ，a，z，，定义为，Γ，a，z，=∫0zta，1e，tdt其中，a为一个大于0的实数参...。
本站公告 2024-09-07 13:33:36
揭秘不完全 Gamma 函数：发现它在数学和统计学中的应用 (不完全真相)
引言不完全Gamma函数是数学和统计学中一个重要的函数，它在许多现实世界问题中都有应用，这个函数通常被视为一个抽象的概念，很难对其含义和应用有一个直观的理解，本文旨在通过实际示例和易于理解的解释来揭示不完全Gamma函数的神秘面纱，不完全Gamma函数的定义不完全Gamma函数，记为Γ，α，x，，是如下积分的定义，Γ，α，x，=∫0x...。
技术教程 2024-09-07 13:30:57
不完全 Gamma 函数：深入了解高级数学中的强大工具 (不完全gamma函数表)
不完全Gamma函数是一个在各种数学和物理学科中应用广泛的高级函数，它可以用来解决一系列问题，从概率和统计到数学物理和工程，定义不完全Gamma函数，记为γ，α，z，，定义为，$$γ，α，z，=\int，0^zt^，α，1，e^，t，dt$$其中α>，0是函数的参数，z是积分的上限，性质不完全Gamma函数具有许多重要的性质，包...。
本站公告 2024-09-07 13:28:22